题目内容
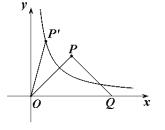
【题目】在平面直角坐标系xOy中,曲线![]() 与x轴交于不同的两点A,B,曲线Γ与y轴交于点C.
与x轴交于不同的两点A,B,曲线Γ与y轴交于点C.
(1)是否存在以AB为直径的圆过点C?若存在,求出该圆的方程;若不存在,请说明理由;
(2)求证:过A,B,C三点的圆过定点,并求出该定点的坐标.
【答案】(1)存在,![]() (2)证明见解析,圆
(2)证明见解析,圆![]() 方程恒过定点
方程恒过定点![]() 或
或![]()
【解析】
(1)将曲线Γ方程中的y=0,得x2﹣mx+2m=0.利用韦达定理求出C,通过![]() 坐标化,求出m得到所求圆的方程.
坐标化,求出m得到所求圆的方程.
(2)设过A,B,C的圆P的方程为(x﹣a)2+(y﹣b)2=r2列出方程组利用圆系方程,推出圆P方程恒过定点即可.
由曲线Γ:y=x2﹣mx+2m(m∈R),
令y=0,得x2﹣mx+2m=0.
设A(x1,0),B(x2,0),
则可得△=m2﹣8m>0,x1+x2=m,x1x2=2m.
令x=0,得y=2m,即C(0,2m).
(1)若存在以AB为直径的圆过点C,则![]() ,得
,得![]() ,
,
即2m+4m2=0,
所以m=0或![]() .由△>0,得m<0或m>8,所以
.由△>0,得m<0或m>8,所以![]() ,
,
此时C(0,﹣1),AB的中点M(![]() ,0)即圆心,半径r=|CM|
,0)即圆心,半径r=|CM|![]()
故所求圆的方程为![]() .
.
(2)设过A,B,C的圆P的方程为(x﹣a)2+(y﹣b)2=r2
满足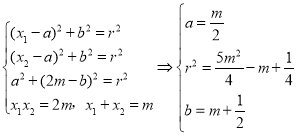
代入P得![]()
展开得(﹣x﹣2y+2)m+x2+y2﹣y=0
当![]() ,即
,即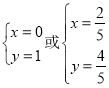 时方程恒成立,
时方程恒成立,
∴圆P方程恒过定点(0,1)或![]() .
.

 优学名师名题系列答案
优学名师名题系列答案【题目】随着旅游观念的转变和旅游业的发展,国民在旅游休闲方面的投入不断增多,民众对旅游的需求也不断提高,安庆某社区居委会统计了2011至2015年每年春节期间外出旅游的家庭数,具体统计资料如表:
年份(x) | 2011 | 2012 | 2013 | 2014 | 2015 |
家庭数(y) | 6 | 10 | 16 | 22 | 26 |
(1)从这5年中随机抽取两年,求外出旅游的家庭至少有1年多于20个的概率;
(2)利用所给数据,求出春节期间外出旅游的家庭数与年份之间的回归直线方程 ![]() ,并判断它们之间是正相关还是负相关;
,并判断它们之间是正相关还是负相关;
(3)利用(2)中所求出的回归直线方程估计该社区2016年在春节期间外出旅游的家庭数.
参考公式: 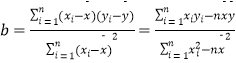 ,
, ![]() .
.