题目内容
【题目】已知函数f(x)=lnx+x2﹣2ax+1(a为常数)
(1)讨论函数f(x)的单调性;
(2)若对任意的a∈(1, ![]() ),都存在x0∈(0,1]使得不等式f(x0)+lna>m(a﹣a2)成立,求实数m的取值范围.
),都存在x0∈(0,1]使得不等式f(x0)+lna>m(a﹣a2)成立,求实数m的取值范围.
【答案】
(1)
解:函数f(x)=lnx+x2﹣2ax+1(a为常数)
f′(x)= ![]() +2x﹣2a=
+2x﹣2a= ![]() ,x>0,
,x>0,
①当a≤0时,f′(x)>0成立,
若f′(x)≥0,则2x2﹣2ax+10≥0,△=4a2﹣8,
当﹣ ![]() 时,f′(x)≥0恒成立,
时,f′(x)≥0恒成立,
所以当a ![]() 时,f(x)在(0,+∞)上单调递增,
时,f(x)在(0,+∞)上单调递增,
②当a ![]() 时,
时,
∵2x2﹣2ax+10≥0,x ![]() 或0
或0 ![]()
2x2﹣2ax+10<0, ![]() ,
,
∴f(x)在(0, ![]() ),(
),( ![]() )上单调递增,
)上单调递增,
在( ![]() ,
, ![]() )单调递减
)单调递减
(2)
∵a∈(1, ![]() ),
), ![]() +2x﹣2a>0,
+2x﹣2a>0,
∴f′(x)>0,f(x)在(0,1]单调递增,
f(x)max=f(1)=2﹣2a,
存在x0∈(0,1]使得不等式f(x0)+lna>m(a﹣a2)成立,
即2﹣2a+lna>m(a﹣a2),
∵任意的a∈(1, ![]() ),
),
∴a﹣a2<0,
即m> ![]() 恒成立,
恒成立,
令g(a)= ![]() ,
,
∵m> ![]() 恒成立 最后化简为g′(a)=
恒成立 最后化简为g′(a)= ![]() =
= ![]()
∵任意的a∈(1, ![]() ),
),
![]() >0,
>0,
∴g(a)= ![]() ,a∈(1,
,a∈(1, ![]() )是增函数.
)是增函数.
∴g(x)<g( ![]() )=
)= ![]() +
+ ![]() =
= ![]()
∴实数m的取值范围m≥ ![]()
【解析】(1)求解f′(x)= ![]() +2x﹣2a=
+2x﹣2a= ![]() ,x>0,判断2x2﹣2ax+10的符号,分类得出①当a≤0时,f′(x)>0成立,当﹣
,x>0,判断2x2﹣2ax+10的符号,分类得出①当a≤0时,f′(x)>0成立,当﹣ ![]() 时,f′(x)≥0恒成立,
时,f′(x)≥0恒成立,
即可得出当a ![]() 时,f(x)在(0,+∞)上单调递增,②当a
时,f(x)在(0,+∞)上单调递增,②当a ![]() 时,求解不等式2x2﹣2ax+10≥0,2x2﹣2ax+10<0,得出f(x)在(0,
时,求解不等式2x2﹣2ax+10≥0,2x2﹣2ax+10<0,得出f(x)在(0, ![]() ),(
),( ![]() )上单调递增,在(
)上单调递增,在( ![]() ,
, ![]() )单调递减,(2)f(x)max=f(1)=2﹣2a,存在x0∈(0,1]使得不等式f(x0)+lna>m(a﹣a2)成立,即2﹣2a+lna>m(a﹣a2),m>
)单调递减,(2)f(x)max=f(1)=2﹣2a,存在x0∈(0,1]使得不等式f(x0)+lna>m(a﹣a2)成立,即2﹣2a+lna>m(a﹣a2),m> ![]() 恒成立,构造函数g(a)=
恒成立,构造函数g(a)= ![]() ,利用导数求解即可转化为最值即可判断.
,利用导数求解即可转化为最值即可判断.
【考点精析】认真审题,首先需要了解利用导数研究函数的单调性(一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减),还要掌握函数的最大(小)值与导数(求函数
在这个区间单调递减),还要掌握函数的最大(小)值与导数(求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值)的相关知识才是答题的关键.
比较,其中最大的是一个最大值,最小的是最小值)的相关知识才是答题的关键.

【题目】已知变量![]() 之间的线性回归方程为
之间的线性回归方程为![]() ,且变量
,且变量![]() 之间的一组相关数据如表所示,则下列说法错误的是( )
之间的一组相关数据如表所示,则下列说法错误的是( )
x | 6 | 8 | 10 | 12 |
y | 6 | m | 3 | 2 |
A. 变量![]() 之间呈现负相关关系
之间呈现负相关关系
B. ![]() 的值等于5
的值等于5
C. 变量![]() 之间的相关系数
之间的相关系数![]()
D. 由表格数据知,该回归直线必过点(9,4)
【题目】随着旅游观念的转变和旅游业的发展,国民在旅游休闲方面的投入不断增多,民众对旅游的需求也不断提高,安庆某社区居委会统计了2011至2015年每年春节期间外出旅游的家庭数,具体统计资料如表:
年份(x) | 2011 | 2012 | 2013 | 2014 | 2015 |
家庭数(y) | 6 | 10 | 16 | 22 | 26 |
(1)从这5年中随机抽取两年,求外出旅游的家庭至少有1年多于20个的概率;
(2)利用所给数据,求出春节期间外出旅游的家庭数与年份之间的回归直线方程 ![]() ,并判断它们之间是正相关还是负相关;
,并判断它们之间是正相关还是负相关;
(3)利用(2)中所求出的回归直线方程估计该社区2016年在春节期间外出旅游的家庭数.
参考公式: 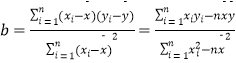 ,
, ![]() .
.
【题目】某学校为了制定治理学校门口上学、放学期间家长接送孩子乱停车现象的措施,对全校学生家长进行了问卷调查.根据从中随机抽取的50份调查问卷,得到了如下的列联表:
同意限定区域停车 | 不同意限定区域停车 | 合计 | |
男 | 20 | 5 | 25 |
女 | 10 | 15 | 25 |
合计 | 30 | 20 | 50 |
则认为“是否同意限定区域停产与家长的性别有关”的把握约为__________.
附:![]() ,其中
,其中![]() .
.
| 0.050 | 0.005 | 0.001 |
| 3.841 | 7.879 | 10.828 |