题目内容
【题目】涡阳县某华为手机专卖店对市民进行华为手机认可度的调查,在已购买华为手机的![]() 名市民中,随机抽取
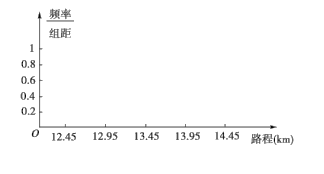
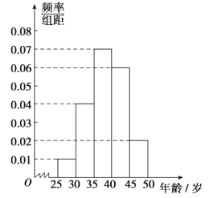
名市民中,随机抽取![]() 名,按年龄(单位:岁)进行统计的频数分布表和频率分布直方图如图:
名,按年龄(单位:岁)进行统计的频数分布表和频率分布直方图如图:

分组(岁) | 频数 |
|
|
|
|
|
|
|
|
|
|
合计 |
|
(1)求频数分布表中![]() 、
、![]() 的值,并补全频率分布直方图;
的值,并补全频率分布直方图;
(2)在抽取的这![]() 名市民中,从年龄在
名市民中,从年龄在![]() 、
、![]() 内的市民中用分层抽样的方法抽取
内的市民中用分层抽样的方法抽取![]() 人参加华为手机宣传活动,现从这
人参加华为手机宣传活动,现从这![]() 人中随机选取
人中随机选取![]() 人各赠送一部华为手机,求这
人各赠送一部华为手机,求这![]() 人中恰有
人中恰有![]() 人的年龄在
人的年龄在![]() 内的概率.
内的概率.
【答案】(1)![]() ,频率分布直方图见解析;(2)
,频率分布直方图见解析;(2)![]() .
.
【解析】
(1)根据分布直方图计算出第二个矩形的面积,乘以![]() 可得出
可得出![]() 的值,再由频数之和为
的值,再由频数之和为![]() 得出
得出![]() 的值,利用频数除以样本容量得出第四个矩形的面积,并计算出第四个矩形的高,于此可补全频率分布直方图;
的值,利用频数除以样本容量得出第四个矩形的面积,并计算出第四个矩形的高,于此可补全频率分布直方图;
(2)先计算出![]() 人中年龄在
人中年龄在![]() 、
、![]() 内的市民人数分别为
内的市民人数分别为![]() 、
、![]() ,将年龄在
,将年龄在![]() 的
的![]() 位市民记为
位市民记为![]() ,年龄在
,年龄在![]() 的
的![]() 位市民记为
位市民记为![]() 、
、![]() 、
、![]() 、
、![]() ,记事件
,记事件![]() 恰有
恰有![]() 人的年龄在
人的年龄在![]() 内,列举出所有的基本事件,并确定事件
内,列举出所有的基本事件,并确定事件![]() 所包含的基本事件数,利用古典概型的概率公式可计算出事件
所包含的基本事件数,利用古典概型的概率公式可计算出事件![]() 的概率.
的概率.
(1)由频数分布表和频率分布直方图可知![]() ,解得
,解得![]() .
.
频率分布直方图中年龄在![]() 内的人数为
内的人数为![]() 人,对应的
人,对应的![]() 为
为![]() ,
,
所以补全的频率分布直方图如下图所示:
(2)由频数分布表知,在抽取的![]() 人中,年龄在
人中,年龄在![]() 内的市民的人数为
内的市民的人数为![]() ,
,
记为![]() ,年龄在
,年龄在![]() 内的市民的人数为
内的市民的人数为![]() ,分别记为
,分别记为![]() 、
、![]() 、
、![]() 、
、![]() .
.
从这![]() 人中任取
人中任取![]() 人的所有基本事件为:
人的所有基本事件为:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,共
,共![]() 个基本事件.
个基本事件.
记“恰有![]() 人的年龄在
人的年龄在![]() 内”为事件
内”为事件![]() ,则
,则![]() 所包含的基本事件有
所包含的基本事件有![]() 个:
个:![]() 、
、![]() 、
、![]() 、
、![]() ,
,
所以这![]() 人中恰有
人中恰有![]() 人的年龄在
人的年龄在![]() 内的概率为
内的概率为![]() .
.

 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案【题目】已知变量![]() 之间的线性回归方程为
之间的线性回归方程为![]() ,且变量
,且变量![]() 之间的一组相关数据如表所示,则下列说法错误的是( )
之间的一组相关数据如表所示,则下列说法错误的是( )
x | 6 | 8 | 10 | 12 |
y | 6 | m | 3 | 2 |
A. 变量![]() 之间呈现负相关关系
之间呈现负相关关系
B. ![]() 的值等于5
的值等于5
C. 变量![]() 之间的相关系数
之间的相关系数![]()
D. 由表格数据知,该回归直线必过点(9,4)
【题目】随着旅游观念的转变和旅游业的发展,国民在旅游休闲方面的投入不断增多,民众对旅游的需求也不断提高,安庆某社区居委会统计了2011至2015年每年春节期间外出旅游的家庭数,具体统计资料如表:
年份(x) | 2011 | 2012 | 2013 | 2014 | 2015 |
家庭数(y) | 6 | 10 | 16 | 22 | 26 |
(1)从这5年中随机抽取两年,求外出旅游的家庭至少有1年多于20个的概率;
(2)利用所给数据,求出春节期间外出旅游的家庭数与年份之间的回归直线方程 ![]() ,并判断它们之间是正相关还是负相关;
,并判断它们之间是正相关还是负相关;
(3)利用(2)中所求出的回归直线方程估计该社区2016年在春节期间外出旅游的家庭数.
参考公式: 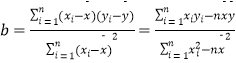 ,
, ![]() .
.