题目内容
【题目】已知函数f(x)=x﹣lnx,g(x)=x2﹣ax.
(1)求函数f(x)在区间[t,t+1](t>0)上的最小值m(t);
(2)令h(x)=g(x)﹣f(x),A(x1 , h(x1)),B(x2 , h(x2))(x1≠x2)是函数h(x)图象上任意两点,且满足 ![]() >1,求实数a的取值范围;
>1,求实数a的取值范围;
(3)若x∈(0,1],使f(x)≥ ![]() 成立,求实数a的最大值.
成立,求实数a的最大值.
【答案】
(1)解: ![]() ,令f'(x)=0,则x=1,
,令f'(x)=0,则x=1,
当t≥1时,f(x)在[t,t+1]上单调递增,f(x)的最小值为f(t)=t﹣lnt;
当0<t<1时,f(x)在区间(t,1)上为减函数,在区间(1,t+1)上为增函数,f(x)的最小值为f(1)=1.
综上,当0<t<1时,m(t)=1;当t≥1时,m(t)=t﹣lnt
(2)解:h(x)=x2﹣(a+1)x+lnx,对于任意的x1,x2∈(0,+∞),不妨取x1<x2,则x1﹣x2<0,
则由 ![]() ,可得h(x1)﹣h(x2)<x1﹣x2,
,可得h(x1)﹣h(x2)<x1﹣x2,
变形得h(x1)﹣x1<h(x2)﹣x2恒成立,
令F(x)=h(x)﹣x=x2﹣(a+2)x+lnx,
则F(x)=x2﹣(a+2)x+lnx在(0,+∞)上单调递增,
故 ![]() 在(0,+∞)恒成立,
在(0,+∞)恒成立,
∴ ![]() 在(0,+∞)恒成立.
在(0,+∞)恒成立.
∵ ![]() ,当且仅当
,当且仅当 ![]() 时取“=”,∴
时取“=”,∴ ![]()
(3)解:∵ ![]() ,∴a(x+1)≤2x2﹣xlnx.
,∴a(x+1)≤2x2﹣xlnx.
∵x∈(0,1],∴x+1∈(1,2],
∴x∈(0,1]使得 ![]() 成立.
成立.
令 ![]() ,则
,则 ![]() ,
,
令y=2x2+3x﹣lnx﹣1,则由 ![]() ,可得
,可得 ![]() 或x=﹣1(舍).
或x=﹣1(舍).
当 ![]() 时,y'<0,则y=2x2+3x﹣lnx﹣1在
时,y'<0,则y=2x2+3x﹣lnx﹣1在 ![]() 上单调递减;
上单调递减;
当 ![]() 时,y'>0,则y=2x2+3x﹣lnx﹣1在
时,y'>0,则y=2x2+3x﹣lnx﹣1在 ![]() 上单调递增.
上单调递增.
∴ ![]() ,∴t'(x)>0在x∈(0,1]上恒成立.
,∴t'(x)>0在x∈(0,1]上恒成立.
∴t(x)在(0,1]上单调递增.则a≤t(1),即a≤1.
∴实数a的最大值为1.
【解析】(1)求出原函数的导函数,得到导函数的零点,分t≥1和0<t<1讨论函数f(x)在区间[t,t+1](t>0)上的单调性,由单调性求得最小值;(2)由 ![]() >1,可得h(x1)﹣x1<h(x2)﹣x2恒成立,构造函数F(x)=h(x)﹣x=x2﹣(a+2)x+lnx,可知F(x)在(0,+∞)上单调递增,由其导函数在(0,+∞)上大于等于0恒成立求得实数a的取值范围;(3)把f(x)≥
>1,可得h(x1)﹣x1<h(x2)﹣x2恒成立,构造函数F(x)=h(x)﹣x=x2﹣(a+2)x+lnx,可知F(x)在(0,+∞)上单调递增,由其导函数在(0,+∞)上大于等于0恒成立求得实数a的取值范围;(3)把f(x)≥ ![]() 变形,分离参数a,然后构造函数
变形,分离参数a,然后构造函数 ![]() ,利用导数求其最大值得答案.
,利用导数求其最大值得答案.
【考点精析】利用函数的最大(小)值与导数对题目进行判断即可得到答案,需要熟知求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值.
比较,其中最大的是一个最大值,最小的是最小值.

【题目】关于函数![]() ,有下列结论:
,有下列结论:
①![]() 的定义域为(-1, 1); ②
的定义域为(-1, 1); ②![]() 的值域为(
的值域为(![]() ,
, ![]() );
);
③![]() 的图象关于原点成中心对称; ④
的图象关于原点成中心对称; ④![]() 在其定义域上是减函数;
在其定义域上是减函数;
⑤对![]() 的定义城中任意
的定义城中任意![]() 都有
都有![]() .
.
其中正确的结论序号为__________.
【题目】某种新产品投放市场一段时间后,经过调研获得了时间![]() (天数)与销售单价
(天数)与销售单价![]() (元)的一组数据,且做了一定的数据处理(如表),并作出了散点图(如图)
(元)的一组数据,且做了一定的数据处理(如表),并作出了散点图(如图)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
表中![]() ,
,![]() .
.
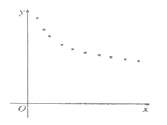
(1)根据散点图判断,![]() 与
与![]() 哪一个更适宜作价格
哪一个更适宜作价格![]() 关于时间
关于时间![]() 的回归方程类型?(不必说明理由)
的回归方程类型?(不必说明理由)
(2)根据判断结果和表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)若该产品的日销售量![]() (件)与时间
(件)与时间![]() 的函数关系为
的函数关系为![]() (
(![]() ),求该产品投放市场第几天的销售额最高?最高为多少元?(结果保留整数)
),求该产品投放市场第几天的销售额最高?最高为多少元?(结果保留整数)
附:对于一组数据![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为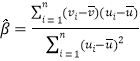 ,
,![]() .
.

