题目内容
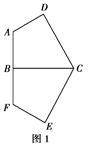
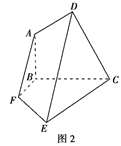
【题目】如图在棱长均为2的正四棱锥P﹣ABCD中,点E为PC中点,则下列命题正确的是( ) 
A.BE平行面PAD,且直线BE到面PAD距离为 ![]()
B.BE平行面PAD,且直线BE到面PAD距离为 ![]()
C.BE不平行面PAD,且BE与平面PAD所成角大于 ![]()
D.BE不平行面PAD,且BE与面PAD所成角小于 ![]()
【答案】D
【解析】解:连接AC,BD,交点为O,以O为坐标原点, OC,OD,OP方向分别x,y,z轴正方向建立空间坐标系,
由正四棱锥P﹣ABCD的棱长均为2,点E为PC的中点,
则O(0,0,0),A(﹣ ![]() ,0,0),B(0,﹣
,0,0),B(0,﹣ ![]() ,0),
,0),
C( ![]() ,0,0),D(0,
,0,0),D(0, ![]() ,0),
,0),
P(0,0, ![]() ),E(
),E( ![]() ,0,
,0, ![]() ),
),
则 ![]() =(
=( ![]() ,
, ![]() ,
, ![]() ),
), ![]() =(﹣
=(﹣ ![]() ,0,﹣
,0,﹣ ![]() ),
),![]() =(0,
=(0, ![]() ,﹣
,﹣ ![]() ),
),
设 ![]() =(x,y,z)是平面PAD的一个法向量,
=(x,y,z)是平面PAD的一个法向量,
则 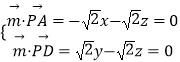 ,
,
取x=1,得 ![]() =(1,﹣1,﹣1),
=(1,﹣1,﹣1),
设BE与平面PAD所成的角为θ,
则sinθ=|cos< ![]() ,
, ![]() >|=|
>|=| ![]() |=
|= ![]() <
< ![]() ,
,
故BE与平面PAD不平行,且BE与平面PAD所成的角小于30°.
由此排除选项A,B,C.
故选:D.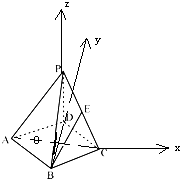
连接AC,BD,交点为O,以O为坐标原点,OC,OD,OP方向分别x,y,z轴正方向建立空间坐标系,分别求出直线BE的方向向量与平面PAD的法向量,代入向量夹角公式,求出BE与平面PAD夹角的正弦值,再由正弦函数的单调性,即可得到答案.

【题目】某种新产品投放市场一段时间后,经过调研获得了时间![]() (天数)与销售单价
(天数)与销售单价![]() (元)的一组数据,且做了一定的数据处理(如表),并作出了散点图(如图)
(元)的一组数据,且做了一定的数据处理(如表),并作出了散点图(如图)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
表中![]() ,
,![]() .
.
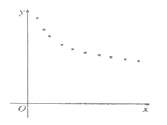
(1)根据散点图判断,![]() 与
与![]() 哪一个更适宜作价格
哪一个更适宜作价格![]() 关于时间
关于时间![]() 的回归方程类型?(不必说明理由)
的回归方程类型?(不必说明理由)
(2)根据判断结果和表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)若该产品的日销售量![]() (件)与时间
(件)与时间![]() 的函数关系为
的函数关系为![]() (
(![]() ),求该产品投放市场第几天的销售额最高?最高为多少元?(结果保留整数)
),求该产品投放市场第几天的销售额最高?最高为多少元?(结果保留整数)
附:对于一组数据![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为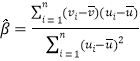 ,
,![]() .
.