题目内容
【题目】甲、乙两人在相同条件下各打靶10次,每次打靶所得的环数如图所示.
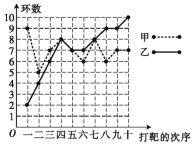
填写下表，请从下列角度对这次结果进行分析.
命中9环及以上的次数 | 平均数 | 中位数 | 方差 | |
甲 | ||||
乙 |
(1)命中9环及以上的次数(分析谁的成绩好些);
(2)平均数和中位数(分析谁的成绩好些);
(3)方差(分析谁的成绩更稳定);
(4)折线图上两人射击命中环数的走势(分析谁更有潜力).
【答案】（1）乙；（2）乙；（3）甲；（4）乙.
【解析】
（1）比较甲乙两人命中9环的次数，即可得到；
（2）由平均数和中位数的概念分析即可得到；
（3）有方差的概念分析即可得到；
（4）从折线图上甲乙两人命中环数的走势分析即可得到.
由题中数据可得如下统计表.
命中9环及以上的次数 | 平均数 | 中位数 | 方差 | |
甲 | 1 | 7 | 7 | 1.2 |
乙 | 3 | 7 | 7.5 | 5.4 |
(1)∵甲乙命中9环及以上的次数分别为1和3次,∴乙的成绩比甲好.
(2)∵甲乙平均数相同,但甲的中位数小于乙的中位数,∴乙的成绩比甲好.
(3)∵
<
,∴甲的成绩更稳定.
(4)∵甲的成绩在平均线上下波动,而乙处于上升趋势,且从第三次后就没有落后于甲,
∴乙更有潜力.
练习册系列答案
相关题目
【题目】某种新产品投放市场一段时间后，经过调研获得了时间
（天数）与销售单价
（元）的一组数据，且做了一定的数据处理（如表），并作出了散点图（如图）
|
|
|
|
|
|
|
|
|
|
|
|
|
|
表中
，
.
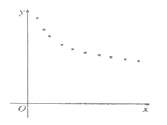
（1）根据散点图判断，
与
哪一个更适宜作价格关于时间的回归方程类型？（不必说明理由）
（2）根据判断结果和表中数据，建立关于的回归方程；
（3）若该产品的日销售量
（件）与时间的函数关系为
（
），求该产品投放市场第几天的销售额最高？最高为多少元？（结果保留整数）
附：对于一组数据
，
，
，
，
，其回归直线
的斜率和截距的最小二乘估计分别为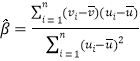
，
.
