题目内容
【题目】设![]() ,
,![]() 或
或![]() ,
,![]() ,
,![]() .
.

![]() 从以下两个命题中任选一个进行证明:
从以下两个命题中任选一个进行证明:
![]() 当
当![]() 时函数
时函数![]() 恰有一个零点;
恰有一个零点;
![]() 当
当![]() 时函数
时函数![]() 恰有一个零点;
恰有一个零点;
![]() 如图所示当
如图所示当![]() 时
时![]() 如
如![]() ,
,![]() 与
与![]() 的图象“好像”只有一个交点,但实际上这两个函数有两个交点,请证明:当
的图象“好像”只有一个交点,但实际上这两个函数有两个交点,请证明:当![]() 时,
时,![]() 与
与![]() 两个交点.
两个交点.
![]() 若方程
若方程![]() 恰有4个实数根,请结合
恰有4个实数根,请结合![]() 的研究,指出实数k的取值范围
的研究,指出实数k的取值范围![]() 不用证明
不用证明![]() .
.
【答案】(1)见解析; (2)见解析; (3)![]() .
.
【解析】
![]() 由函数的零点及方程的根的关系得:当
由函数的零点及方程的根的关系得:当![]() 时,令
时,令![]() ,解得:
,解得:![]() ,即函数
,即函数![]() 恰有一个零点,且此零点为2,再用判别式判断函数的零点个数
恰有一个零点,且此零点为2,再用判别式判断函数的零点个数
![]() 由二次方程区间根的问题得:
由二次方程区间根的问题得:![]() ,由韦达定理得:
,由韦达定理得:![]() ,
,![]() ,所以
,所以![]() ,
,![]() .
.
![]() 结合
结合![]() 的研究,实数k的取值范围为:
的研究,实数k的取值范围为:![]() ,得解
,得解
![]() 当
当![]() 时,
时,![]() ,
,
令![]() ,解得:
,解得:![]() ,
,
即函数![]() 恰有一个零点,且此零点为2,
恰有一个零点,且此零点为2,
![]() 证明:当
证明:当![]() 时,
时,![]() ,
,
令![]() ,解得:
,解得:![]() ,
,
所以函数![]() 恰有一个零点,且此零点为
恰有一个零点,且此零点为![]() ,
,
![]() ,
,
所以![]() ,
,
又![]() ,
,
所以![]() ,
,
所以方程![]() ,有两个不等实数根,记为
,有两个不等实数根,记为![]() ,
,![]() ,
,
由韦达定理得:![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,
,
即![]() ,
,![]() ,
,
所以当![]() 时,
时,![]() 与
与![]() 两个交点.
两个交点.
![]() 结合
结合![]() 的研究,实数k的取值范围为:
的研究,实数k的取值范围为:![]() ,
,
故答案为:![]() .
.


练习册系列答案
相关题目
【题目】某种新产品投放市场一段时间后,经过调研获得了时间![]() (天数)与销售单价
(天数)与销售单价![]() (元)的一组数据,且做了一定的数据处理(如表),并作出了散点图(如图)
(元)的一组数据,且做了一定的数据处理(如表),并作出了散点图(如图)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
表中![]() ,
,![]() .
.
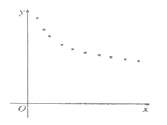
(1)根据散点图判断,![]() 与
与![]() 哪一个更适宜作价格
哪一个更适宜作价格![]() 关于时间
关于时间![]() 的回归方程类型?(不必说明理由)
的回归方程类型?(不必说明理由)
(2)根据判断结果和表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)若该产品的日销售量![]() (件)与时间
(件)与时间![]() 的函数关系为
的函数关系为![]() (
(![]() ),求该产品投放市场第几天的销售额最高?最高为多少元?(结果保留整数)
),求该产品投放市场第几天的销售额最高?最高为多少元?(结果保留整数)
附:对于一组数据![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为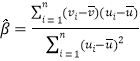 ,
,![]() .
.


