题目内容
(本小题满分12分)
已知数列{an}的前n项和Sn=12n-n2,求数列{|an|}的前n项和Tn.
剖析:由Sn=12n-n2知Sn是关于n的无常数项的二次函数(n∈N*),可知{an}为等差数列,求出an,然后再判断哪些项为正,哪些项为负,最后求出Tn.
已知数列{an}的前n项和Sn=12n-n2,求数列{|an|}的前n项和Tn.
剖析:由Sn=12n-n2知Sn是关于n的无常数项的二次函数(n∈N*),可知{an}为等差数列,求出an,然后再判断哪些项为正,哪些项为负,最后求出Tn.
解:当n=1时,a1=S1=12-12=11;
当n≥2时,an=Sn-Sn-1=12n-n2-[12(n-1)-(n-1)2]=13-2n.
∵n=1时适合上式,
∴{an}的通项公式为an=13-2n.
由an=13-2n≥0,得n≤
 ,
,即当 1≤n≤6(n∈N*)时,an>0;当n≥7时,an<0.
(1)当 1≤n≤6(n∈N*)时,
Tn=|a1|+|a2|+…+|an|=a1+a2+…+an=12n-n2.
(2)当n≥7(n∈N*)时,
Tn=|a1|+|a2|+…+|an|=(a1+a2+…+a6)-(a7+a8+…+an)=-(a1+a2+…+an)+2(a1+…+a6)
=-Sn+2S6=n2-12n+72.∴Tn=


略

练习册系列答案
相关题目
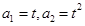 (t>0且t≠1).若
(t>0且t≠1).若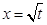 是函数
是函数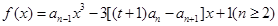 的一个极值点.
的一个极值点.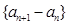 是等比数列,并求数列
是等比数列,并求数列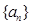 的通项公式;
的通项公式;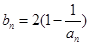 ,当t=2时,数列
,当t=2时,数列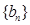 的前n项和为Sn,求使Sn>2008的n的最小值;
的前n项和为Sn,求使Sn>2008的n的最小值;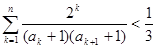 。
。 ,数列
,数列 和
和 满足:
满足: ,
, ,函数
,函数 的图像在点
的图像在点 处的切线在
处的切线在 轴上的截距为
轴上的截距为 .
.  }的通项公式;
}的通项公式; 的项中仅
的项中仅 最小,求
最小,求 的取值范围;
的取值范围;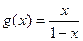 ,令函数
,令函数 数列
数列 满足:
满足: 且
且 证明:
证明: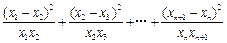
 .
.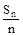 }的前10项和为
}的前10项和为 中,
中, ,则数列
,则数列 的最小项的值为 ( )
的最小项的值为 ( )



 ,公比为
,公比为 的等比数列,设
的等比数列,设 (n
(n N*),数列{
N*),数列{ }满足
}满足
 }的通项公式;
}的通项公式;
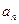 }满足
}满足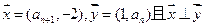 ,
,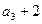 是
是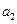 与
与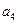 的等差中项.
的等差中项. 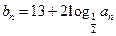 ,
, ,求
,求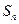 的最大值.
的最大值. 满足
满足 ,则
,则