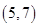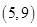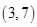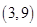题目内容
在△ABC中,角A,B,C所对的边分别为a,b,c,已知向量m=(cos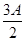 ,sin
,sin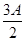 ),n=(cos
),n=(cos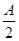 ,sin
,sin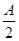 ),且满足|m+n|=
),且满足|m+n|=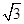 .
.
(1)求角A的大小;
(2)若|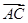 |+|
|+|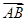 |=
|=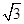 |
| |,试判断△ABC的形状.
|,试判断△ABC的形状.
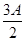 ,sin
,sin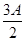 ),n=(cos
),n=(cos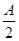 ,sin
,sin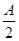 ),且满足|m+n|=
),且满足|m+n|=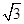 .
.(1)求角A的大小;
(2)若|
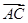 |+|
|+|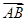 |=
|=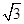 |
| |,试判断△ABC的形状.
|,试判断△ABC的形状.(1)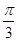 (2)直角三角形
(2)直角三角形
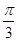 (2)直角三角形
(2)直角三角形解:(1)由|m+n|=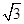 ,
,
得m2+n2+2m·n=3,
即1+1+2(cos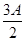 cos
cos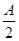 +sin
+sin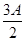 sin
sin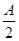 )=3,
)=3,
∴cosA=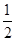 .
.
∵0<A<π,∴A=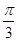 .
.
(2)∵|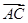 |+|
|+|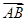 |=
|=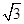 |
| |,
|,
∴sinB+sinC=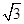 sinA,
sinA,
∴sinB+sin(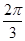 -B)=
-B)=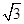 ×
×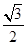 ,
,
即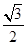 sinB+
sinB+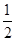 cosB=
cosB=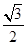 ,
,
∴sin(B+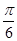 )=
)=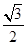 .
.
∵0<B<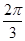 ,∴
,∴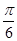 <B+
<B+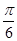 <
<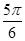 ,
,
∴B+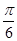 =
=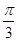 或
或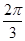 ,故B=
,故B=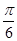 或
或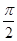 .
.
当B=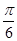 时,C=
时,C=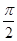 ;当B=
;当B=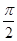 时,C=
时,C=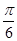 .
.
故△ABC是直角三角形.
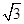 ,
,得m2+n2+2m·n=3,
即1+1+2(cos
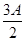 cos
cos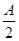 +sin
+sin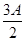 sin
sin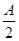 )=3,
)=3,∴cosA=
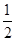 .
.∵0<A<π,∴A=
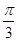 .
.(2)∵|
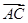 |+|
|+|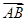 |=
|=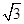 |
| |,
|,∴sinB+sinC=
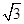 sinA,
sinA,∴sinB+sin(
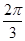 -B)=
-B)=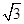 ×
×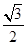 ,
,即
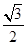 sinB+
sinB+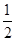 cosB=
cosB=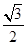 ,
,∴sin(B+
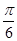 )=
)=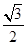 .
.∵0<B<
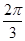 ,∴
,∴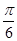 <B+
<B+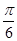 <
<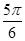 ,
,∴B+
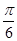 =
=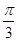 或
或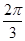 ,故B=
,故B=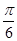 或
或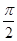 .
.当B=
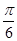 时,C=
时,C=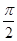 ;当B=
;当B=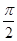 时,C=
时,C=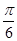 .
.故△ABC是直角三角形.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
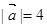 ,
,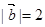 ,且
,且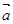 与
与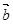 夹角为
夹角为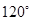 ,求
,求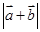 ;
; 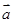 与
与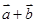 的夹角.
的夹角.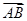 =
=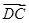 =(1,1),
=(1,1),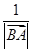 ·
·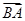 +
+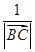 ·
·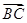 =
=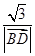 ·
·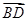 ,则四边形ABCD的面积为________.
,则四边形ABCD的面积为________.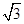 ,|
,|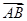 +
+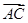 |=|
|=|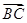 |,则
|,则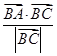 =________.
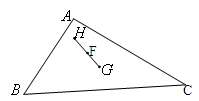
=________.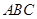 的重心、垂心,F为线段GH的中点,若△
的重心、垂心,F为线段GH的中点,若△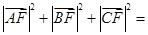 .
.
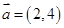 ,
,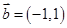 ,则
,则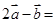 ( )
( )