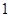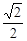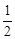题目内容
已知直线x+y+m=0与圆x2+y2=4交于不同的两点A,B,O是坐标原点,
+
|≥|
|,则实数m的取值范围是( )
| |OA |
| OB |
| AB |
| A.[-2,2] | B.[2,2
| ||||
C.(-2
| D.[2,2
|
∵直线x+y+m=0与圆x2+y2=4交于不同的两点A,B,
故AB为圆的一条弦,且圆心O(0,0),半径r=2,
设线段AB的中点为C,根据向量加法的平行四边形法则,可得
+
=2
,
∴
+
|≥|
|,即为2|
|≥|
|,即|
|≥
|
|=AC,
根据圆中弦的性质,则△OAC为直角三角形,
∴在Rt△OAC中,OA=r=2,OC≥AC,
∴
≤OC<2,
∵OC为点O到直线x+y+m=0的距离,
故OC=
=
,
∴
≤
<2,即
,解得m∈(-2
,-2]∪[2,2
),
∴实数m的取值范围是(-2
,-2]∪[2,2
).
故选:B.
故AB为圆的一条弦,且圆心O(0,0),半径r=2,
设线段AB的中点为C,根据向量加法的平行四边形法则,可得
| OA |
| OB |
| OC |
∴
| |OA |
| OB |
| AB |
| OC |
| AB |
| OC |
| 1 |
| 2 |
| AB |
根据圆中弦的性质,则△OAC为直角三角形,
∴在Rt△OAC中,OA=r=2,OC≥AC,
∴
| 2 |
∵OC为点O到直线x+y+m=0的距离,
故OC=
| |0+0+m| | ||
|
| |m| | ||
|
∴
| 2 |
| |m| | ||
|
|
| 2 |
| 2 |
∴实数m的取值范围是(-2
| 2 |
| 2 |
故选:B.

练习册系列答案
 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
 +
+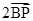 +
+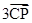 =
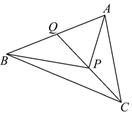
=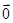 ,设Q为CP延长线与AB的交点,求证:
,设Q为CP延长线与AB的交点,求证: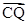 =
=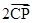 .
.
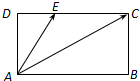
 中,
中, 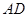 是
是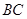 边上的高,给出下列结论:
边上的高,给出下列结论: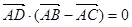 ; ②
; ②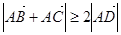 ; ③
; ③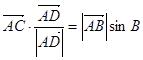 ;
; 

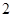
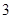
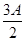 ,sin
,sin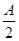 ,sin
,sin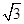 .
.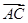 |+|
|+|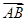 |=
|= |,试判断△ABC的形状.
|,试判断△ABC的形状.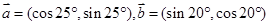 ,若
,若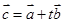 (
(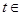
 ),则
),则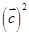 的最小值为( )
的最小值为( )