题目内容
已知向量a=(1,2),b=(2,-2).
(1)设c=4a+b,求(b·c)a;
(2)若a+λb与a垂直,求λ的值;
(3)求向量a在b方向上的投影.
(1)设c=4a+b,求(b·c)a;
(2)若a+λb与a垂直,求λ的值;
(3)求向量a在b方向上的投影.
(1)0 (2)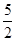 (3)-
(3)-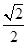
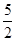 (3)-
(3)-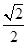
解:(1)∵a=(1,2),b=(2,-2),
∴c=4a+b=(4,8)+(2,-2)=(6,6).
∴b·c=2×6-2×6=0,
∴(b·c)a=0a=0.
(2)a+λb=(1,2)+λ(2,-2)=(2λ+1,2-2λ),
由于a+λb与a垂直,
∴2λ+1+2(2-2λ)=0,∴λ=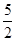 .
.
∴λ的值为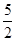 .
.
(3)设向量a与b的夹角为θ,向量a在b方向上的投影为|a|cosθ.
∴|a|cosθ=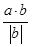 =
= =-
=-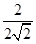 =-
=-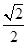 .
.
∴c=4a+b=(4,8)+(2,-2)=(6,6).
∴b·c=2×6-2×6=0,
∴(b·c)a=0a=0.
(2)a+λb=(1,2)+λ(2,-2)=(2λ+1,2-2λ),
由于a+λb与a垂直,
∴2λ+1+2(2-2λ)=0,∴λ=
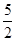 .
.∴λ的值为
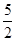 .
.(3)设向量a与b的夹角为θ,向量a在b方向上的投影为|a|cosθ.
∴|a|cosθ=
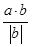 =
= =-
=-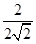 =-
=-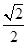 .
.
练习册系列答案
相关题目

 的值;
的值;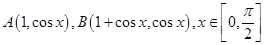 ,
,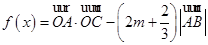 的最小值为
的最小值为 ,求实数m的值.
,求实数m的值.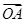 ·
·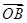 =0,存在实数λ,μ,使得
=0,存在实数λ,μ,使得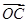 =λ
=λ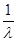 +
+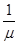 =1
=1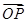 =3a+2b,
=3a+2b,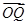 =a+3b,则P,Q两点间的距离为( )
=a+3b,则P,Q两点间的距离为( )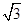

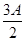 ,sin
,sin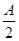 ,sin
,sin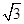 .
.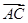 |+|
|+|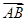 |=
|= |,试判断△ABC的形状.
|,试判断△ABC的形状.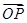 =x
=x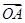 +y
+y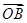 ,且
,且 =2
=2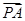 ,则( )
,则( )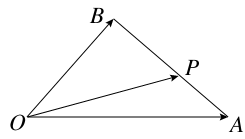
 ,y=
,y=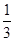
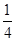 ,y=
,y=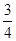
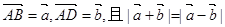 ,则四边形ABCD的形状
,则四边形ABCD的形状 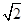
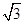
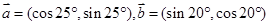 ,若
,若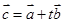 (
(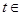
 ),则
),则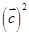 的最小值为( )
的最小值为( )