题目内容
【题目】已知不等式
(1)若
，求不等式的解集；
(2)若已知不等式的解集不是空集，求实数
的取值范围。
【答案】（1）
；（2）
【解析】分析：（1）当a=1时，把要解的不等式等价转化为与之等价的三个不等式组，求出每个不等式组的解集，再取并集，即得所求；
（2）利用函数图像可知f（x）的最小值为1，故2a＞1，由此求得求得a的取值范围．
详解：(1) 若a=1，不等式即 2|x﹣3|+|x﹣4|＜2，①若x≥4，则3x﹣10＜2，x＜4，∴舍去．
②若3＜x＜4，则x﹣2＜2，∴3＜x＜4．③若x≤3，则10﹣3x＜2，∴
．
综上，不等式的解集为
．
(2)设f(x)＝2|x－3|＋|x－4|，则
，
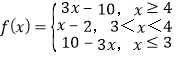作出函数f(x)的图象，如图所示．
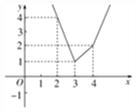
由图象可知，f(x)≥1，
∴2a>1，a>
，即a的取值范围为.
练习册系列答案
相关题目
