题目内容
若关于x的方程
-mx-2=0有两个不相等的实数解,则实数m的取值范围是( )
| 2x-x2 |
A.(-∞,-
| B.(-∞,-
| ||||||
C.(
| D.[-1,-
|
关于x的方程
-mx-2=0有两个不相等的实数解,
即是y=
,y=mx+2的图象有两个交点
因为y=
是以(1,0)为圆心,1为半径的上半圆,
而y=mx+2是过定点(0,2)的直线,由图可知,
当直线在AB和AC之间时符合要求,
当直线为AB时 m=
=-1,
当直线为 AC时,有点D到直线AC的距离等于半径可得m=±
(正值舍去)
故实数m的取值范围是[-1,-
),
故选 D
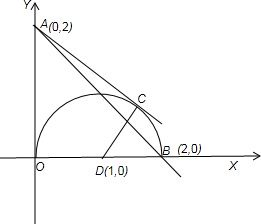
| 2x-x2 |
即是y=
| 2x-x2 |
因为y=
| 2x-x2 |
而y=mx+2是过定点(0,2)的直线,由图可知,
当直线在AB和AC之间时符合要求,
当直线为AB时 m=
| 2-0 |
| 0-2 |
当直线为 AC时,有点D到直线AC的距离等于半径可得m=±
| 3 |
| 4 |
故实数m的取值范围是[-1,-
| 3 |
| 4 |
故选 D
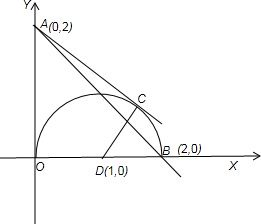

练习册系列答案
相关题目