题目内容
9.若函数f(n)属于自然数的增函数,f[f(n)]=3n,则f(10)=19.分析 结合题设条件,利用列举法一一验证,能够求出f(10)的值
解答 解:若f(1)=1,则f(f(1))=f(1)=1,与条件f(f(n))=3n矛盾,故不成立;
若f(1)=3,则f(f(1))=f(3)=3,进而f(f(3))=f(3)=9,与前式矛盾,故不成立;
若f(1)=n(n>3),则f(f(1))=f(n)=3,与f(x)单调递增矛盾.
所以只剩f(1)=2.验证之:
f(f(1))=f(2)=3,
进而f(f(2))=f(3)=6,
进而f(f(3))=f(6)=9,
由单调性以及f(n)属于自然数,f(4)=7,f(5)=8,
所以f[f(4)]=f(7)=12,f[f(5)]=f(8)=15,f[f(6)]=f(9)=18,
f[f(7)]=f(12)=21,所以f(10)=19;
故答案为:19.
点评 本题考查函数值的求法,解题时要认真审题,仔细解答,注意列举法、分类讨论思想的合理运用.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
1.某程序框图如图所示,该程序运行后输出的S的值是( )
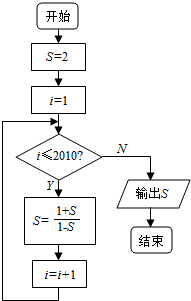

| A. | 2 | B. | -3 | C. | $\frac{1}{3}$ | D. | -$\frac{1}{2}$ |
18.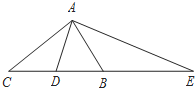 在△ABC中,∠BAC=90°,D是BC边的中点,AE⊥AD,AE交CB的延长线于E,则下面结论中正确的是( )
在△ABC中,∠BAC=90°,D是BC边的中点,AE⊥AD,AE交CB的延长线于E,则下面结论中正确的是( )
 在△ABC中,∠BAC=90°,D是BC边的中点,AE⊥AD,AE交CB的延长线于E,则下面结论中正确的是( )
在△ABC中,∠BAC=90°,D是BC边的中点,AE⊥AD,AE交CB的延长线于E,则下面结论中正确的是( )| A. | △AED∽△ACB | B. | △AEB∽△ACD | C. | △BAE∽△ACE | D. | △AEC∽△DAC |
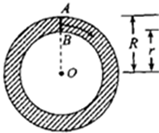 如图,我们知道圆环是线段AB绕圆心O旋转一周所形成的平面图形,所以,圆环的面积S=π(R2-r2)=(R-r)×2π×$\frac{R+r}{2}$可以看作是以线段AB=R-r为宽,以AB的中心绕圆心O旋转一周所形成的圆的周长2π×$\frac{R+r}{2}$为长的矩形面积.请将上述想法拓展到空间,并解决下列问题:若将平面区域M={(x,y)|(x-2)2+y2≤1}绕y轴旋转一周,则所形成的旋转体的体积是4π2.
如图,我们知道圆环是线段AB绕圆心O旋转一周所形成的平面图形,所以,圆环的面积S=π(R2-r2)=(R-r)×2π×$\frac{R+r}{2}$可以看作是以线段AB=R-r为宽,以AB的中心绕圆心O旋转一周所形成的圆的周长2π×$\frac{R+r}{2}$为长的矩形面积.请将上述想法拓展到空间,并解决下列问题:若将平面区域M={(x,y)|(x-2)2+y2≤1}绕y轴旋转一周,则所形成的旋转体的体积是4π2.