题目内容
18．
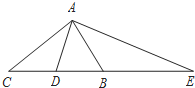在△ABC中，∠BAC=90°，D是BC边的中点，AE⊥AD，AE交CB的延长线于E，则下面结论中正确的是（ ）| A． | △AED∽△ACB | B． | △AEB∽△ACD | C． | △BAE∽△ACE | D． | △AEC∽△DAC |
分析 先利用直角三角形斜边上的中线等于斜边的一半得到DA=DC，则∠DAC=∠C，再利用等角的余角相等得到∠EAB=∠DAC，从而有∠EAB=∠C，再加上公共角即可判断△BAE∽△ACE．
解答 解：∵∠BAC=90°，D是BC中点，
∴DA=DC，
∴∠DAC=∠C，
又∵AE⊥AD，
∴∠EAB+∠BAD=90°，∠CAD+∠BAD=90°，
∴∠EAB=∠DAC，
∴∠EAB=∠C，
而∠E是公共角，
∴△BAE∽△ACE
故选C．
点评 此题主要考查学生对相似三角形判定定理的掌握和应用．
练习册系列答案
孟建平小学滚动测试系列答案
黄冈天天练口算题卡系列答案
相关题目
6．6本相同的数学书和3本相同的语文书分给9个人，每人1本，共有不同分法（ ）
| A． | C${\;}_{9}^{3}$ | B． | A${\;}_{9}^{3}$ | C． | A${\;}_{9}^{6}$ | D． | A${\;}_{9}^{3}$•A${\;}_{3}^{3}$ |
10．函数y=sin2（$\frac{ω}{2}$x-$\frac{π}{4}$）（ω＞0）的最小正周期为π，则ω为（ ）
| A． | 2 | B． | $\frac{1}{2}$ | C． | 4 | D． | $\frac{1}{4}$ |
7．某中学对高二甲、乙两个同类班级，进行“加强‘语文阅读理解’训练，对提高‘数学应用题’得分率的作用”的试验，其中甲班为试验班（加强语文阅读理解训练），乙班为对比班（常规教学，无额外训练），在试验前的测试中，甲、乙两班学生在数学应用题上的得分率基本一致，试验结束后，统计几次数学应用题测试的平均成绩（均取整数）如下表所示：
现规定平均成绩在80分以上（不含80分）的为优秀．
（I）试分析估计两个班级的优秀率；
（Ⅱ）由以上统计数据填写下面2x2列联表，根据以上数据，能杏有95%的把握认为“加强‘语文阅读理解’训练对提高‘数学应用题’得分率”有帮助？
参考公式及数据：x2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$
| 60分以下 | 61-70分 | 71-80分 | 81-90分 | 91-100分 | |
| 甲班（人数） | 3 | 6 | 11 | 18 | |
| 12乙班（人数） | 7 | 13 | 10 | 10 | 10 |
（I）试分析估计两个班级的优秀率；
（Ⅱ）由以上统计数据填写下面2x2列联表，根据以上数据，能杏有95%的把握认为“加强‘语文阅读理解’训练对提高‘数学应用题’得分率”有帮助？
| 优秀人数 | 非优秀人数 | 合计 | |
| 甲班 | |||
| 乙班 | |||
| 合计 |
| P（x2≥k0） | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.028 | 0.010 | 0.005 | 0.001 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
8．若（2+x）7=a0+a1（x+1）+a2（x+1）2+…+a7（x+1）7，则a1+a3+a5+a7等于（ ）
| A． | $\frac{127}{2}$ | B． | $\frac{255}{2}$ | C． | 64 | D． | 128 |