题目内容
在椭圆 中,左焦点为
中,左焦点为 , 右顶点为
, 右顶点为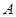 , 短轴上方端点为
, 短轴上方端点为 ,若
,若 ,则该椭圆的离心率为___________.
,则该椭圆的离心率为___________.

 中,左焦点为
中,左焦点为 , 右顶点为
, 右顶点为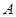 , 短轴上方端点为
, 短轴上方端点为 ,若
,若 ,则该椭圆的离心率为___________.
,则该椭圆的离心率为___________.
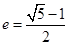
试题分析:由题意,得
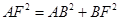 ,∴
,∴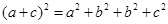 .∵
.∵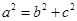 ,∴
,∴ ,∴
,∴ ,∴
,∴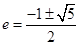 .又∵
.又∵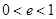 ,∴
,∴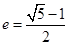 .
.
练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
题目内容
 中,左焦点为
中,左焦点为 , 右顶点为
, 右顶点为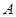 , 短轴上方端点为
, 短轴上方端点为 ,若
,若 ,则该椭圆的离心率为___________.
,则该椭圆的离心率为___________.
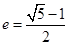
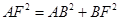 ,∴
,∴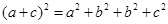 .∵
.∵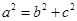 ,∴
,∴ ,∴
,∴ ,∴
,∴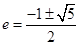 .又∵
.又∵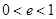 ,∴
,∴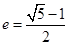 .
.
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案