题目内容
已知椭圆 (
( )的短轴长为2,离心率为
)的短轴长为2,离心率为 .过点M(2,0)的直线
.过点M(2,0)的直线 与椭圆
与椭圆 相交于
相交于 、
、 两点,
两点, 为坐标原点.
为坐标原点.
(1)求椭圆 的方程;
的方程;
(2)求 的取值范围;
的取值范围;
(3)若 点关于
点关于 轴的对称点是
轴的对称点是 ,证明:直线
,证明:直线 恒过一定点.
恒过一定点.
 (
( )的短轴长为2,离心率为
)的短轴长为2,离心率为 .过点M(2,0)的直线
.过点M(2,0)的直线 与椭圆
与椭圆 相交于
相交于 、
、 两点,
两点, 为坐标原点.
为坐标原点.(1)求椭圆
 的方程;
的方程;(2)求
 的取值范围;
的取值范围;(3)若
 点关于
点关于 轴的对称点是
轴的对称点是 ,证明:直线
,证明:直线 恒过一定点.
恒过一定点.(1) .(2)
.(2) .(3)直线
.(3)直线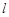 过定点
过定点 .
.
 .(2)
.(2) .(3)直线
.(3)直线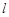 过定点
过定点 .
.试题分析:(1)由已知得
 ,得
,得 .
.(2)设
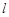 :
: ,与椭圆
,与椭圆 的方程联立,消去
的方程联立,消去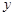 得
得 .由△>0得
.由△>0得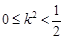 .
.设
 ,则
,则 .
.将

表示成为

由
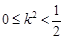 ,求得范围是
,求得范围是 .
.(3)由对称性可知N
 ,定点在
,定点在 轴上.
轴上.在直线方程AN:
 中,令
中,令 得:
得: ,得证.
,得证.试题解析:(1)易知
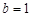 ,
, 得
得 ,故
,故 .
.故方程为
 .(3分)
.(3分)(2)设
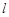 :
: ,与椭圆
,与椭圆 的方程联立,消去
的方程联立,消去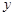 得
得 .由△>0得
.由△>0得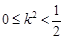 .
.设
 ,则
,则 .
.∴

 =
=
 ,∴
,∴ ,
,故所求范围是
 .(8分)
.(8分)(3)由对称性可知N
 ,定点在
,定点在 轴上.
轴上.直线AN:
 ,令
,令 得:
得: ,
,∴直线
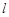 过定点
过定点 .(13分)
.(13分)
练习册系列答案
相关题目
 与圆
与圆 相切,且与圆
相切,且与圆 相内切,记圆心
相内切,记圆心 ;设
;设 为曲线
为曲线 轴上的动点,
轴上的动点, 为坐标原点,过点
为坐标原点,过点 作
作 的平行线交曲线
的平行线交曲线 两个不同的点.
两个不同的点. 和
和 的比值能否为一个常数?若能,求出这个常数,若不能,请说明理由;
的比值能否为一个常数?若能,求出这个常数,若不能,请说明理由; 的面积为
的面积为 ,
, 的面积为
的面积为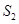 ,令
,令 ,求
,求 的最大值.
的最大值.
 经过点
经过点 ,其左、右顶点分别是
,其左、右顶点分别是 、
、 ,左、右焦点分别是
,左、右焦点分别是 、
、 ,
, (异于
(异于 交直线
交直线 于
于 、
、 两点,若
两点,若 成等比数列.
成等比数列.
 为直径的圆过点
为直径的圆过点 的长轴在
的长轴在 轴上,焦距为
轴上,焦距为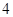 ,则
,则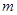 等于 ( )
等于 ( )



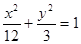 的焦点为
的焦点为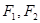 ,点
,点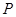 在椭圆上,如果线段
在椭圆上,如果线段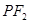 的中点在
的中点在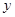 轴上,那么
轴上,那么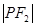 是
是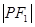 的( )
的( ) 倍
倍 倍
倍 倍
倍 倍
倍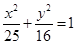 的长轴的端点、焦点,则双曲线C的方程为_______.
的长轴的端点、焦点,则双曲线C的方程为_______. 的中心在原点、焦点在
的中心在原点、焦点在 轴上,抛物线
轴上,抛物线 的顶点在原点、焦点在
的顶点在原点、焦点在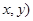 .由于记录失误,使得其中恰有一个点既不在椭圆
.由于记录失误,使得其中恰有一个点既不在椭圆










