题目内容
(2013•浙江)设△ABC,P0是边AB上一定点,满足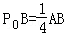 ,且对于边AB上任一点P,恒有
,且对于边AB上任一点P,恒有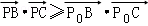 则( )
则( )
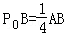 ,且对于边AB上任一点P,恒有
,且对于边AB上任一点P,恒有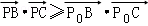 则( )
则( )| A.∠ABC=90° | B.∠BAC=90° | C.AB=AC | D.AC=BC |
D
以AB所在的直线为x轴,以AB的中垂线为y轴建立直角坐标系,设AB=4,C(a,b),P(x,0)
则BP0=1,A(﹣2,0),B(2,0),P0(1,0)
∴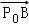 =(1,0),
=(1,0),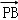 =(2﹣x,0),
=(2﹣x,0),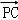 =(a﹣x,b),
=(a﹣x,b),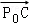 =(a﹣1,b)
=(a﹣1,b)
∵恒有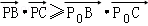
∴(2﹣x)(a﹣x)≥a﹣1恒成立
整理可得x2﹣(a+2)x+a+1≥0恒成立
∴△=(a+2)2﹣4(a+1)≤0
即△=a2≤0
∴a=0,即C在AB的垂直平分线上
∴AC=BC
故△ABC为等腰三角形
故选D
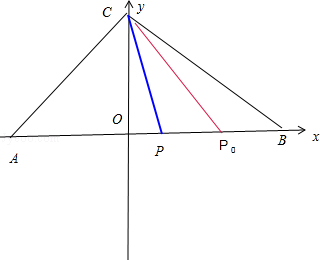
则BP0=1,A(﹣2,0),B(2,0),P0(1,0)
∴
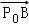 =(1,0),
=(1,0),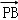 =(2﹣x,0),
=(2﹣x,0),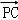 =(a﹣x,b),
=(a﹣x,b),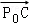 =(a﹣1,b)
=(a﹣1,b)∵恒有
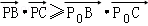
∴(2﹣x)(a﹣x)≥a﹣1恒成立
整理可得x2﹣(a+2)x+a+1≥0恒成立
∴△=(a+2)2﹣4(a+1)≤0
即△=a2≤0
∴a=0,即C在AB的垂直平分线上
∴AC=BC
故△ABC为等腰三角形
故选D


练习册系列答案
相关题目
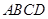 的边长为
的边长为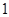 ,
,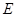 在
在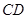 延长线上,且
延长线上,且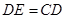 .动点
.动点 从点
从点 出发,沿正方形
出发,沿正方形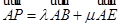 ,则下列命题正确的是 .(填上所有正确命题的序号)
,则下列命题正确的是 .(填上所有正确命题的序号)
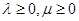 ;
;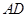 中点时,
中点时,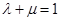 ;
;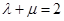 ,则点
,则点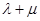 的最大值为
的最大值为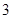 ;
;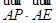 的最大值为
的最大值为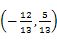 ,θ为a与b的夹角.
,θ为a与b的夹角.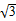 sin2(θ-x),求f(x)的单调递增区间.
sin2(θ-x),求f(x)的单调递增区间. 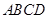 中,
中,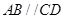 ,
,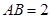 ,
,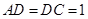 ,
,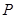 是线段
是线段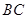 上一动点,
上一动点,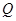 是线段
是线段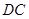 上一动点,
上一动点,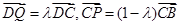 ,则
,则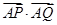 的取值范围是 .
的取值范围是 .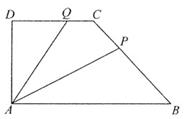
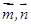 满足:对任意的
满足:对任意的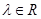 ,恒有
,恒有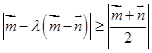 ,则( )
,则( )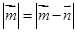
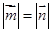
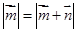
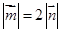
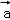 =(3,0),
=(3,0),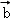 =(0,1),若
=(0,1),若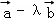 与
与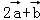 共线,则实数的λ值为( )
共线,则实数的λ值为( )
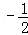
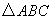 所在平面内的一点,且满足
所在平面内的一点,且满足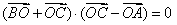 ,则
,则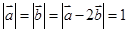 ,则
,则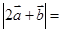 .
.