题目内容
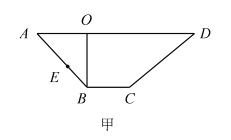
【题目】如图甲所示, ![]() 是梯形
是梯形![]() 的高,
的高, ![]() ,
, ![]() ,
, ![]() ,现将梯形
,现将梯形![]() 沿
沿![]() 折起如图乙所示的四棱锥
折起如图乙所示的四棱锥![]() ,使得
,使得![]() ,点
,点![]() 是线段
是线段![]() 上一动点.
上一动点.
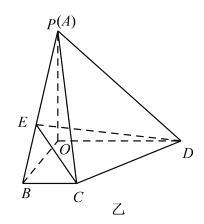
(1)证明: ![]() 和
和![]() 不可能垂直;
不可能垂直;
(2)当![]() 时,求
时,求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)详见解析; (2)![]() .
.
【解析】试题分析:由于折叠后![]() ,经过计算知
,经过计算知![]() ,这样
,这样![]() 两两垂直,因此以它们为坐标轴建立空间直角坐标系,写出各点坐标.
两两垂直,因此以它们为坐标轴建立空间直角坐标系,写出各点坐标.
(1)否定性命题,可假设![]() ,同时设
,同时设![]() (
(![]() ),利用向量垂直计算出
),利用向量垂直计算出![]() ,如果满足
,如果满足![]() 说明存在,如果不满足
说明存在,如果不满足![]() 说明不存在;
说明不存在;
(2)由![]() 得
得![]() 点坐标,从而可求出平面
点坐标,从而可求出平面![]() 的法向量
的法向量![]() ,则向量
,则向量![]() 与
与![]() 夹角的余弦的绝对值等于直线
夹角的余弦的绝对值等于直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
解析:如图甲所示,因为![]() 是梯形
是梯形![]() 的高,
的高,![]() ,所以
,所以![]() ,因为
,因为![]() ,
,![]() ,可得
,可得![]() ,
,![]() ,如图乙所示,
,如图乙所示,![]() ,
, ![]() ,
,![]() ,所以有
,所以有![]() ,所以
,所以![]() ,而
,而![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() ,又
,又![]() ,所以
,所以![]() 、
、![]() 、
、![]() 两两垂直.故以
两两垂直.故以![]() 为原点,建立空间直角坐标系(如图),则
为原点,建立空间直角坐标系(如图),则![]() ,
,![]() ,
,![]() ,
,

(1)设![]() 其中
其中![]() ,所以
,所以![]() ,
,![]() ,假设
,假设![]() 和
和![]() 垂直,则
垂直,则![]() ,有
,有![]() ,解得
,解得![]() ,这与
,这与![]() 矛盾,假设不成立,所以
矛盾,假设不成立,所以![]() 和
和![]() 不可能垂直.
不可能垂直.
(2)因为![]() ,所以
,所以 ![]() ,设平面
,设平面![]() 的一个法向量是
的一个法向量是![]() ,因为
,因为![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,即
,即 ,取
,取![]() ,而
,而![]() ,所以
,所以 ,所以
,所以![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
【题目】某种产品的广告费支出![]() (百万元)与销售额
(百万元)与销售额![]() (百万元)之间有如下对应数据:
(百万元)之间有如下对应数据:
| 2 | 4 | 5 | 6 | 8 |
| 30 | 40 | 50 | 60 | 70 |
如果![]() 与
与![]() 之间具有线性相关关系.
之间具有线性相关关系.
(1)作出这些数据的散点图;
(2)求这些数据的线性回归方程![]() ;
;
(3)预测当广告费支出为9百万元时的销售额。 ( 参考数据: ![]() )
)
【题目】假设某种设备使用的年限x(年)与所支出的维修费用y(万元)有以下统计资料:
使用年限x | 2 | 3 | 4 | 5 | 6 |
维修费用y | 2 | 4 | 5 | 6 | 7 |
若由资料知y对x呈线性相关关系。试求:
(1)求![]() ; (2)线性回归方程
; (2)线性回归方程![]() ;
;
(3)估计使用10年时,维修费用是多少?
附:利用“最小二乘法”计算a,b的值时,可根据以下公式: