题目内容
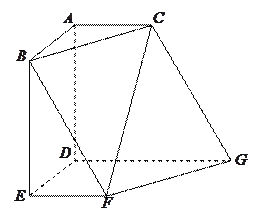
【题目】如图,多面体![]() 中,
中, ![]() 两两垂直,平面
两两垂直,平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
, ![]() .
.
(1)证明四边形![]() 是正方形;
是正方形;
(2)判断点![]() 是否四点共面,并说明为什么?
是否四点共面,并说明为什么?
(3)连结![]() ,求证:
,求证: ![]() 平面
平面![]() .
.
【答案】(1)见解析;(2)共面,见解析;(3)见解析
【解析】试题分析:(1)要证明四边形是一个正方形,首先证明四边形是一个平行四边形,这里应用两个平面平行的性质定理,再根据一对邻边相等,得到正方形.
(2)要判断四点共面,只要判断三点共面,再证明第四个点在平面上,或者是证明四点在两条平行的直线上,选择后者,进行证明.
(3)要证明限于面垂直只要证明这条线与平面上的两条相交直线垂直,解题的关键是找出这两条线,选择了BG和BD这两条相交直线,得到结论.
试题解析:
证明:(1) ,
,
同理AD∥BE,
则四边形ABED是平行四边形.
又AD⊥DE,AD=DE,
∴四边形ABED是正方形
(2)取DG中点P,连接PA,PF.
在梯形EFGD中,FP∥DE且FP=DE.
又AB∥DE且AB=DE,∴AB∥PF且AB=PF
∴四边形ABFP为平行四边形,
∴AP∥BF
在梯形ACGD中,AP∥CG,∴BF∥CG,
∴B,C,F,G四点共面
(3)同(1)中证明方法知四边形BFGC为平行四边形.
且有AC∥DG、EF∥DG,从而AC∥EF,
∴EF⊥AD,BE∥AD
又BE=AD=2、EF=1故![]() ,而
,而![]() ,
,
故四边形BFGC为菱形,CF⊥BG
又由AC∥EF且AC=EF知CF∥AE.
正方形ABED中,AE⊥BD,故CF⊥BD.
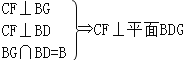

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目