题目内容
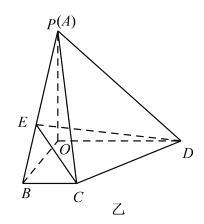
【题目】设点M是棱长为2的正方体的棱AD的中点,P是平面![]() 内一点,若面
内一点,若面![]() 分别与面ABCD和面
分别与面ABCD和面![]() 所成的锐二面角相等,则
所成的锐二面角相等,则![]() 长度的最小值是( )
长度的最小值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 1
D. 1
【答案】A
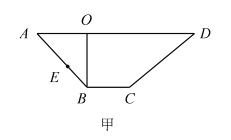
【解析】如图,过点![]() 作
作![]() 的平行线交
的平行线交![]() 于点
于点![]() 、交
、交![]() 于点
于点![]() ,连接
,连接![]() ,
,
则![]() 是平面
是平面![]() 与平面
与平面![]() 的交线,
的交线, ![]() 是平面
是平面![]() 与平面
与平面![]() 的交线.
的交线. ![]() ,交
,交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 垂直
垂直![]() 于点
于点![]() ,则有
,则有![]() 与平面
与平面![]() 垂直,
垂直,
所以, ![]()
![]() ,即角
,即角![]() 是平面
是平面![]() 与平面
与平面![]() 的所成二面角的平面角,
的所成二面角的平面角,
且![]()
![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,
,
同上有: ![]() ,且有
,且有![]() ,又因为
,又因为![]() ,故
,故![]()
而![]() ,故
,故![]() ,
,
而四边形![]() 一定是平行四边形,故它还是菱形,即点
一定是平行四边形,故它还是菱形,即点![]() 一定是
一定是![]() 的中点,
的中点,
点![]() 长度的最小值是点
长度的最小值是点![]() 到直线
到直线![]() 的距离,
的距离,
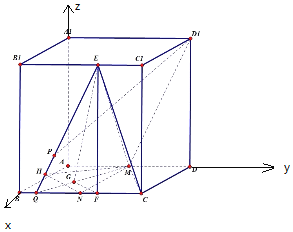
以![]() 为原点,
为原点, ![]() 为
为![]() 轴,
轴, ![]() 为
为![]() 轴,
轴, ![]() 为
为![]() 轴,建立空间直角坐标系,
轴,建立空间直角坐标系,![]()
![]()
∴![]() 长度的最小值
长度的最小值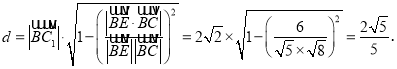
故选A.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目