题目内容
15.某班决定举行联欢会迎接元旦,小明负责游戏环节,他设计了一个“击球猜谜”的游戏,需要先在长为6米的绳子上挂上两个气球.(1)若这两个小球挂在绳子的6等分点处,求两个气球相邻的概率;(两个气球不能挂在同一个等分点).
(2)若其中一个气球挂在绳子的左起第一个三等分点处,求两个气球之间的距离不小于1米的概率.
分析 (1)设绳子的5个6等分点的标号为1,2,3,4,5,利用列举法结合古典概型的概率公式进行求解即可.
(2)求出满足两个气球之间的距离不小于1米条件,结合几何概型的概率公式进行求解即可.
解答 解:(1)令两个气球相邻的事件为A,
绳子的5个6等分点的标号为1,2,3,4,5,
这两个小球挂在绳子的6等分点处所有的可能有(1,2),(1,3),(1,4),(1,5),(2,3),(2,4),(2,5),(3,4),(3,5),(4,5)共有10种,
则两个气球相邻的有(1,2),(2,3),(3,4),(4,5)共有4种,
则两个气球相邻的概率为P(A)=$\frac{4}{10}=\frac{2}{5}$.
(2)设两个气球之间的距离不小于1米的事件为B.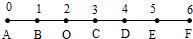
如图其中一个气球挂在绳子的左起第一个三等分点处O,令BO=CO=1,
若两个气球之间的距离不小于1米,
则另外一个球应该挂着AB之间或者CF之间,
∵|AB|=1,|CF|=3,
∴|AB|+|CF|=1+3=4,
则两个气球之间的距离不小于1米的概率P(B)=$\frac{4}{6}=\frac{2}{3}$.
点评 本题主要考查古典概型和几何概型的概率的计算,利用列举法是解决古典概型的常用方法.

练习册系列答案
相关题目
5.若复数z满足$\frac{z}{1+2i}$=|3-4i|,则z的共轭复数$\overline{z}$对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
10.四边形OABC中,$\overrightarrow{CB}=\frac{1}{2}\overrightarrow{OA}$,若$\overrightarrow{OA}=\overrightarrow a$,$\overrightarrow{OC}=\overrightarrow b$,则$\overrightarrow{AB}$=( )
| A. | $\overrightarrow a-\frac{1}{2}\overrightarrow b$ | B. | $\frac{\overrightarrow a}{2}-\overrightarrow b$ | C. | $\overrightarrow b+\frac{\overrightarrow a}{2}$ | D. | $\overrightarrow b-\frac{1}{2}\overrightarrow a$ |
7.已知数列{an}为等比数列,a2=2,a5=$\frac{1}{4}$,则a1a2+a2a3+…+anan+1=( )
| A. | 16(1-$\frac{1}{{2}^{n}}$) | B. | 16(1-$\frac{1}{{4}^{n}}$) | C. | $\frac{32}{3}$(1-$\frac{1}{{2}^{n}}$) | D. | $\frac{32}{3}$(1-$\frac{1}{{4}^{n}}$) |