题目内容
7.已知数列{an}为等比数列,a2=2,a5=$\frac{1}{4}$,则a1a2+a2a3+…+anan+1=( )| A. | 16(1-$\frac{1}{{2}^{n}}$) | B. | 16(1-$\frac{1}{{4}^{n}}$) | C. | $\frac{32}{3}$(1-$\frac{1}{{2}^{n}}$) | D. | $\frac{32}{3}$(1-$\frac{1}{{4}^{n}}$) |
分析 通过q3=$\frac{{a}_{5}}{{a}_{2}}$可得公比和首项,进而可得anan+1=$(\frac{1}{2})^{2n-5}$,进而可得数列{anan+1}是以8为首项,$\frac{1}{4}$为公比的等比数列,计算即得结论.
解答 解:∵a2=2,a5=$\frac{1}{4}$,∴q3=$\frac{{a}_{5}}{{a}_{2}}$=$\frac{1}{8}$,
∴q=$\frac{1}{2}$,a1=$\frac{{a}_{2}}{q}$=4,
∴数列{an}的通项为:an=4•$(\frac{1}{2})^{n-1}$=$(\frac{1}{2})^{n-3}$;
则anan+1=$(\frac{1}{2})^{n-3}$•$(\frac{1}{2})^{n-2}$=$(\frac{1}{2})^{2n-5}$,
又∵a1a2=$(\frac{1}{2})^{2-5}$=8,
∴数列{anan+1}是以8为首项,$\frac{1}{4}$为公比的等比数列,
∴a1a2+a2a3+…+anan+1=8•$\frac{1-\frac{1}{{4}^{n}}}{1-\frac{1}{4}}$=$\frac{32}{3}$(1-$\frac{1}{{4}^{n}}$).
故选:D
点评 本题考查求等比数列的通项的应用以及数列求和,考查学生的计算能力,属于中档题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
2.有如下命题:命题p:设集合M={x|0<x≤3},N={x|0<x≤2},则“a∈M”是“a∈N”的充分而不必要条件;命题q:“?x0∈R,x02-x0-1>0”的否定是“?x∈R,x2-x-1≤0”,则下列命题中为真命题的是( )
| A. | p∧q | B. | p∧(¬q) | C. | p∨q | D. | p∨(¬q) |
12.$\int_{-\frac{π}{4}}^{\frac{π}{4}}{(2{{cos}^2}\frac{x}{2}+tanx)}dx$=( )
| A. | $\frac{π}{2}+\sqrt{2}$ | B. | $\sqrt{2}$ | C. | $\frac{π}{2}$ | D. | $π+\sqrt{2}$ |
16.据如图的流程图可得结果为( )
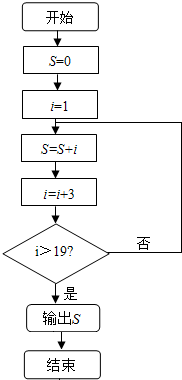

| A. | 19 | B. | 67 | C. | 51 | D. | 70 |
 已知等差数列{an}中,a3=7,a6=16,将此等差数列的各项排成如下三角形数阵:则此数阵中第20行从左到右的第10个数是598.
已知等差数列{an}中,a3=7,a6=16,将此等差数列的各项排成如下三角形数阵:则此数阵中第20行从左到右的第10个数是598.