题目内容
4.已知a,b,c分别为△ABC三个内角A,B,C的对边长,且(2c-b)cosA=acosB.(1)求角A的大小;
(2)若a=2,求△ABC面积S的最大值.
分析 (1)利用正弦定理化简已知等式,利用两角和与差的正弦函数公式及诱导公式化简,根据sinC不为0求出cosA的值,即可确定出A的度数.
(2)利用正弦定理,结合辅助角公式,表示出面积,即可求△ABC面积S的最大值.
解答 解:(1)利用正弦定理可得(2sinC-sinB)cosA=sinAcosB,
则2sinCcosA=sin(A+B)=sinC,
所以$cosA=\frac{1}{2}$,故$A=\frac{π}{3}$----(5分)
(2)由$\frac{b}{sinB}=\frac{c}{sinC}=\frac{a}{sinA}$得$b=\frac{{4\sqrt{3}}}{3}sinB,c=\frac{{4\sqrt{3}}}{3}sinC$,
所以$S=\frac{1}{2}bcsinA=\frac{{4\sqrt{3}}}{3}sinBsinC=\frac{{4\sqrt{3}}}{3}sinBsin(\frac{2π}{3}-B)$
=$2sinBcosB+\frac{{2\sqrt{3}}}{3}{sin^2}B=\frac{2}{{\sqrt{3}}}(\frac{{\sqrt{3}}}{2}sin2B-\frac{1}{2}cos2B)+\frac{{\sqrt{3}}}{3}$=$\frac{{2\sqrt{3}}}{3}sin(2B-\frac{π}{6})+\frac{{\sqrt{3}}}{3}$,
∵$0<B<\frac{2π}{3},-\frac{π}{6}<2B-\frac{π}{6}<\frac{7π}{6}$,
∴$-\frac{1}{2}<sin(2B-\frac{π}{6})≤1,0<\frac{{2\sqrt{3}}}{3}sin(2B-\frac{π}{6})+\frac{{\sqrt{3}}}{3}≤\frac{{3\sqrt{3}}}{3}$,
∴△ABC面积S的最大值为$\frac{3\sqrt{3}}{3}$--12分
点评 此题考查了正弦定理,两角和与差的正弦函数公式,诱导公式,以及特殊角的三角函数值,熟练掌握正弦定理是解本题的关键.

| A. | $\frac{π}{2}+\sqrt{2}$ | B. | $\sqrt{2}$ | C. | $\frac{π}{2}$ | D. | $π+\sqrt{2}$ |
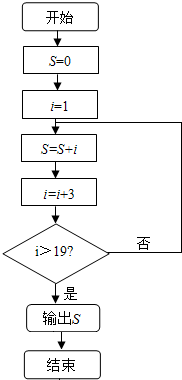
| A. | 19 | B. | 67 | C. | 51 | D. | 70 |
| A. | 20 | B. | 180 | C. | 45 | D. | -10 |