题目内容
6.已知递增等差数列{an}满足:a1=2,a1,a2,a3成等比数列(Ⅰ)求{an}通项公式
(Ⅱ)若数列{bn}满足bn+1-bn=an+2,且b1=2,设数列{$\frac{1}{{b}_{n}}$}的前n项和Tn,求证:Tn<1.
分析 (I)设递增等差数列{an}的公差为d>0,由a1=2,a1,a2,a4成等比数列,可得$\left\{\begin{array}{l}{{a}_{1}=2}\\{({a}_{1}+d)^{2}={a}_{1}({a}_{1}+3d)}\end{array}\right.$,解得即可.
(II)bn+1-bn=an+2=2(n+1),且b1=2,利用“累加求和”可得bn=(bn-bn-1)+(bn-1-bn-2)+…+(b2-b1)+b1,再利用“裂项求和”即可得出.
解答 (I)解:设递增等差数列{an}的公差为d>0,
∵a1=2,a1,a2,a4成等比数列,
∴$\left\{\begin{array}{l}{{a}_{1}=2}\\{({a}_{1}+d)^{2}={a}_{1}({a}_{1}+3d)}\end{array}\right.$,解得$\left\{\begin{array}{l}{{a}_{1}=2}\\{d=2}\end{array}\right.$,
∴an=2+2(n-1)=2n.
(II)证明:∵bn+1-bn=an+2=2(n+1),且b1=2,
∴bn=(bn-bn-1)+(bn-1-bn-2)+…+(b2-b1)+b1
=2n+2(n-1)+…+2×2+2=$2×\frac{n(n+1)}{2}$=n(n+1),
∴$\frac{1}{{b}_{n}}$=$\frac{1}{n(n+1)}$=$\frac{1}{n}-\frac{1}{n+1}$,
∴前n项和Tn=$(1-\frac{1}{2})+(\frac{1}{2}-\frac{1}{3})$+…+$(\frac{1}{n}-\frac{1}{n+1})$=1-$\frac{1}{n+1}$<1.
∴Tn<1.
点评 本题考查了等差数列与等比数列的通项公式及其前n项和公式、“累加求和”、“放缩法”,考查了推理能力与计算能力,属于中档题.

 53天天练系列答案
53天天练系列答案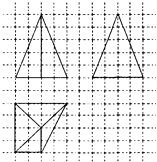 如图,网格纸上小止方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的体积为( )
如图,网格纸上小止方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的体积为( )| A. | 16 | B. | 20 | C. | 4$\sqrt{29}$ | D. | 60 |
| A. | x2=$\frac{1}{2}$y | B. | x2=y | C. | x2=2y | D. | x2=4y |
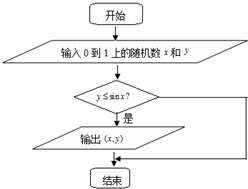 由计算机产生的两个0到1上的随机数,按右侧流程图所示的规则,则能输出数对(x,y)的概率是1-cos1.
由计算机产生的两个0到1上的随机数,按右侧流程图所示的规则,则能输出数对(x,y)的概率是1-cos1.