题目内容
11.已知x,y∈R+,且x+y=2(Ⅰ)要使不等式$\frac{1}{x}$+$\frac{1}{y}$≥|a+2|-|a-1|恒成立,求实数a的取值范围
(Ⅱ)求证:x2+2y2$≥\frac{8}{3}$.
分析 (Ⅰ)由$\frac{1}{x}$+$\frac{1}{y}$=($\frac{1}{x}$+$\frac{1}{y}$)•$\frac{x+y}{2}$=1+$\frac{y}{2x}$+$\frac{x}{2y}$,利用基本不等式求得它的最小值为2,再由2≥|a+2|-|a-1|,利用绝对值的意义求得实数a的取值范围.
(Ⅱ)由柯西不等式得(x2+2y2)•(1+$\frac{1}{2}$)≥(x+y)2=4,由此变形即可证得要证的结论.
解答 解:(Ⅰ)∵x,y∈R+,且x+y=2,∴$\frac{1}{x}$+$\frac{1}{y}$=($\frac{1}{x}$+$\frac{1}{y}$)•$\frac{x+y}{2}$=1+$\frac{y}{2x}$+$\frac{x}{2y}$≥2,
当且仅当x=y=1时,取等号.
要使不等式$\frac{1}{x}$+$\frac{1}{y}$≥|a+2|-|a-1|恒成立,只要2≥|a+2|-|a-1|.
而|a+2|-|a-1|表示数轴上的a对应点到-2的距离减去它到1对应点的距离,而$\frac{1}{2}$对应点到-2的距离减去它到1对应点的距离正好等于2,
故不等式2≥|a+2|-|a-1|的解集为(-∞,$\frac{1}{2}$).
(Ⅱ)证明:由柯西不等式得(x2+2y2)•(1+$\frac{1}{2}$)≥(x+y)2=4,∴x2+2y2≥$\frac{8}{3}$.
点评 本题主要考查基本不等式、柯西不等式的应用,绝对值的意义,绝对值不等式的解法,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.已知$\frac{m}{1+i}$=1-ni,其中m,n是实数,i是虚数单位,则m+n=( )
| A. | 3 | B. | 2 | C. | 1 | D. | -1 |
2.若p:0<x<2是q:a-1<x≤a的必要不充分条件,则a的取值范围是( )
| A. | [1,2] | B. | [1,2) | C. | [1,2) | D. | (1,2] |
19.已知1≤a≤3,2≤b≤5,则方程x2-bx+a2=0有实数解的概率是( )
| A. | $\frac{3}{8}$ | B. | $\frac{2}{3}$ | C. | $\frac{5}{8}$ | D. | $\frac{1}{3}$ |
16.函数f(x)=$\left\{\begin{array}{l}{x-sinx,x>0}\\{{x}^{2}-2014x-2015,x≤0}\end{array}\right.$的零点个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
3.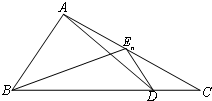 如图,已知点D为△ABC的边BC上一点,$\overrightarrow{BD}=3\overrightarrow{DC}$,En(n∈N+)为边AC上的一列点,满足$\overrightarrow{{E_n}A}=\frac{1}{4}{a_{n+1}}\overrightarrow{{E_n}B}-(3{a_n}+2)\overrightarrow{{E_n}D}$,其中实数列{an}中
如图,已知点D为△ABC的边BC上一点,$\overrightarrow{BD}=3\overrightarrow{DC}$,En(n∈N+)为边AC上的一列点,满足$\overrightarrow{{E_n}A}=\frac{1}{4}{a_{n+1}}\overrightarrow{{E_n}B}-(3{a_n}+2)\overrightarrow{{E_n}D}$,其中实数列{an}中
an>0,a1=1,则{an}的通项公式为( )
 如图,已知点D为△ABC的边BC上一点,$\overrightarrow{BD}=3\overrightarrow{DC}$,En(n∈N+)为边AC上的一列点,满足$\overrightarrow{{E_n}A}=\frac{1}{4}{a_{n+1}}\overrightarrow{{E_n}B}-(3{a_n}+2)\overrightarrow{{E_n}D}$,其中实数列{an}中
如图,已知点D为△ABC的边BC上一点,$\overrightarrow{BD}=3\overrightarrow{DC}$,En(n∈N+)为边AC上的一列点,满足$\overrightarrow{{E_n}A}=\frac{1}{4}{a_{n+1}}\overrightarrow{{E_n}B}-(3{a_n}+2)\overrightarrow{{E_n}D}$,其中实数列{an}中an>0,a1=1,则{an}的通项公式为( )
| A. | 2•3n-1-1 | B. | 2n-1 | C. | 3n-2 | D. | 3•2n-1-2 |
20.下列四个命题中,正确的是( )
| A. | 若平面α∥平面β,直线m∥平面α,则m∥β | |
| B. | 若平面α⊥平面γ,且平面β⊥平面γ,则α∥β | |
| C. | 平面α⊥平面β,其α∩β=l,点A∈α,A∉l,若直线AB⊥l,则AB⊥β | |
| D. | 直线m,n为异面直线,且m⊥平面α,n⊥平面β,若m⊥n,则α⊥β |