题目内容
15．已知等差数列{an}的前n项和为Sn，且满足：a2+a4=14，S7=70．（1）求数列{an}的通项公式；
（2）设Tn=2Sn-7n，求Tn的最小值．
分析 （1）根据题意列方程组求得首项和公差，进而求得数列的通项公式．
（2）根据等差数列求和公式求得Tn的表达式，利用二次函数的性质确定其最小值．
解答 解：（1）设等差数列的公差为d，依题意得$\left\{\begin{array}{l}{2{a}_{1}+4d=14}\\{7{a}_{1}+21d=70}\end{array}\right.$，解之得a1=1，d=3，
∴an=1+（n-1）•3=3n-2．
（2）Tn=2Sn-7n=2•$\frac{n}{2}[1+3n-2]$-7n=3n2-8n，
∵n∈N*，
∴当n=1时，Tn有最小值-5．
点评 本题主要考查了等差数列的性质和通项公式．考查了学生对数列基础公式的灵活运用．
练习册系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
3．
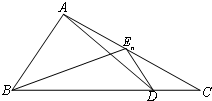如图，已知点D为△ABC的边BC上一点，$\overrightarrow{BD}=3\overrightarrow{DC}$，En（n∈N+）为边AC上的一列点，满足$\overrightarrow{{E_n}A}=\frac{1}{4}{a_{n+1}}\overrightarrow{{E_n}B}-（3{a_n}+2）\overrightarrow{{E_n}D}$，其中实数列{an}中
an＞0，a1=1，则{an}的通项公式为（ ）
如图，已知点D为△ABC的边BC上一点，$\overrightarrow{BD}=3\overrightarrow{DC}$，En（n∈N+）为边AC上的一列点，满足$\overrightarrow{{E_n}A}=\frac{1}{4}{a_{n+1}}\overrightarrow{{E_n}B}-（3{a_n}+2）\overrightarrow{{E_n}D}$，其中实数列{an}中an＞0，a1=1，则{an}的通项公式为（ ）
| A． | 2•3n-1-1 | B． | 2n-1 | C． | 3n-2 | D． | 3•2n-1-2 |
10．计算$\frac{2i}{1-i}$（i为虚数单位）等于（ ）
| A． | -1+i | B． | -1-i | C． | 1-i | D． | 1+i |
20．下列四个命题中，正确的是（ ）
| A． | 若平面α∥平面β，直线m∥平面α，则m∥β | |
| B． | 若平面α⊥平面γ，且平面β⊥平面γ，则α∥β | |
| C． | 平面α⊥平面β，其α∩β=l，点A∈α，A∉l，若直线AB⊥l，则AB⊥β | |
| D． | 直线m，n为异面直线，且m⊥平面α，n⊥平面β，若m⊥n，则α⊥β |
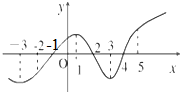已知函数y=f（x）的导函数f′（x）的图象如图所示，则函数f（x）在区间[-3，5]上取得极大值时，x的取值为2．