题目内容
7.已知集合A={x|x2+y2=1},B={y|y=cos2x},则( )| A. | A∩B={(0,1)} | B. | A=B | C. | A∩B=ϕ | D. | A∩B=B |
分析 求出A中x的范围确定出A,求出B中y的范围确定出B,求出A与B的交集,即可做出判断.
解答 解:由A中x2+y2=1,得到x∈[-1,1],即A=[-1,1];
由B中y=cos2x,得到y∈[0,1],即B=[0,1],
则A∩B=[0,1]=B,
故选:D.
点评 此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.

练习册系列答案
相关题目
18.函数y=f(x)的图象如图所示,则以下描述正确的是( )
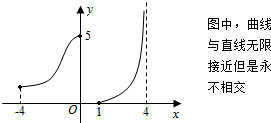

| A. | 函数f(x)的定义域为[-4,4) | |
| B. | 函数f(x)的值域为[0,5] | |
| C. | 此函数在定义域内既不是增函数也不是减函数 | |
| D. | 对于任意的y∈[0,+∞),都有唯一的自变量x与之对应 |
2.已知cosα=$\frac{3}{5}$,则sin($\frac{π}{2}$-α)=( )
| A. | $\frac{3}{5}$ | B. | -$\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | -$\frac{4}{5}$ |
12.m,n为实数,命题p:m+n>2;命题q:m>1且n>1,则p是q的( )
| A. | 充分不必要的条件 | B. | 必要不充分的条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要的条件 |
16.对两个变量y和x进行回归分析,得到一组样本数据:(x1,y1),(x2,y2),…,(xn,yn),则下列说法中不正确的是( )
| A. | 由样本数据得到的回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$必过样本中心($\overline{x}$,$\overline{y}$) | |
| B. | 残差平方和越小的模型,拟合的效果越好 | |
| C. | 用相关指数R2来刻画回归效果,R2越小,说明模型的拟合效果越好 | |
| D. | 两个随机变量的线性相关性越强,相关系数的绝对值越接近于1 |