题目内容
2.已知矩阵M=$(\begin{array}{l}{1}&{m}\\{n}&{1}\end{array})$,若向量$(\begin{array}{l}{-2}\\{1}\end{array})$在矩阵M的变换下得到向量$(\begin{array}{l}{1}\\{3}\end{array})$.(Ⅰ) 求矩阵M;
(Ⅱ) 设矩阵$N(\begin{array}{l}{1}&{0}\\{2}&{1}\end{array})$,求直线x-y+1=0在矩阵NM的对应变换作用下得到的曲线C的方程.
分析 (Ⅰ)利用矩阵变换公式,即可求矩阵N;
(Ⅱ)求出MN,可得坐标之间的关系,代人直线x+y+1=0整理,即可求曲线的方程
解答 解:(Ⅰ)由=$(\begin{array}{l}{1}&{m}\\{n}&{1}\end{array})$$(\begin{array}{l}{-2}\\{1}\end{array})$=$[\begin{array}{l}{1}\\{3}\end{array}]$…(1分)
得$\left\{\begin{array}{l}{-2+m=1}\\{-2n+1=3}\end{array}\right.$,解得$\left\{\begin{array}{l}{n=-1}\\{m=3}\end{array}\right.$…(2分)
∴M=$[\begin{array}{l}{1}&{3}\\{-1}&{1}\end{array}]$…(3分)
(Ⅱ)NM=$[\begin{array}{l}{1}&{0}\\{2}&{1}\end{array}][\begin{array}{l}{1}&{3}\\{-1}&{1}\end{array}]$=$[\begin{array}{l}{1}&{3}\\{1}&{7}\end{array}]$…(4分)
设点(x,y)是直线x-y+1上1一点,在矩阵NM的对应变换作用下得到的点(x′,y′),则
$[\begin{array}{l}{1}&{3}\\{1}&{7}\end{array}]$$[\begin{array}{l}{x}\\{y}\end{array}]$=$[\begin{array}{l}{x′}\\{y′}\end{array}]$,可得$\left\{\begin{array}{l}{x+3y=x′}\\{x+7y=y′}\end{array}\right.$…(5分)
∴$\left\{\begin{array}{l}{y=\frac{y′-x′}{4}}\\{x=\frac{7x′-3y′}{4}}\end{array}\right.$,代入x-y+1=0得2x′-y′+1=0…(6分)
即所求的曲线方程为2x-y-1=0…(7分)
点评 本题给出矩阵变换,求直线x+y+1=0在矩阵NM的对应变换作用下得到的曲线方程,着重考查了矩阵与变换的运算、曲线方程的求法等知识,属于中档题.

| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |
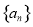 的公差为
的公差为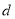 ,前
,前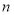 项和为
项和为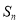 ,若
,若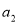 ,
,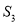 ,
,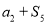 成等比数列,则
成等比数列,则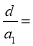 ( )
( )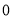 B.
B.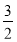
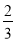 D.
D.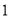
 点P是在平面直角坐标系中不在x轴上的一个动点,满足:过点P可作抛物线x2=y的两条切线,切点分别为A,B.
点P是在平面直角坐标系中不在x轴上的一个动点,满足:过点P可作抛物线x2=y的两条切线,切点分别为A,B. 4月10日,2015《中国汉字听写大会》全国巡回赛正式启动,并拉开第三届“汉听大会”全国海选的帷幕.某市为了了解本市高中学生的汉字书写水平,在全市范围内随机抽取了近千名学生参加汉字听写考试,将所得数据整理后,绘制出频率分布直方图如图所示.
4月10日,2015《中国汉字听写大会》全国巡回赛正式启动,并拉开第三届“汉听大会”全国海选的帷幕.某市为了了解本市高中学生的汉字书写水平,在全市范围内随机抽取了近千名学生参加汉字听写考试,将所得数据整理后,绘制出频率分布直方图如图所示.