题目内容
17.已知等比数列{an}满足:an>0,a1=5,Sn为其前{an}项和,且20S1,S3,7S2成等差数列.(1)求数列{an}的通项公式;
(2)设bn=log5a1+log5a2+…+log5an,求数列{$\frac{1}{b_n}$}的前n项和Tn.
分析 (1)通过20S1,S3,7S2成等差数列可得公比,进而可得结论;
(2)通过对数的运算性质及分离分母,并项相加即可.
解答 解:(1)设数列{an}的公比为q,
∵20S1,S3,7S2成等差数列,∴2S3=20S1+7S2.
即$2({a_1}+{a_1}q+{a_1}{q^2})=20{a_1}+7({a_1}+{a_1}q)$,
化简得2q2-5q-25=0,
解得:q=5或$q=-\frac{5}{2}$,
∵an>0,∴$q=-\frac{5}{2}$不符合题意,舍去,
∴${a_n}={a_1}{q^{n-1}}=5×{5^{n-1}}={5^n}$.
(2)∵bn=log5a1+log5a2+…+log5an
=${log_5}({a_1}{a_2}…{a_n})={log_5}{5^{1+2+3+…+n}}=1+2+3+…+n$
=$\frac{n(n+1)}{2}$,
∴$\frac{1}{b_n}$=$\frac{2}{n(n+1)}=2(\frac{1}{n}-\frac{1}{n+1})$,
∴${T_n}=\frac{1}{b_1}+\frac{1}{b_2}+…+\frac{1}{b_n}$=$2[(1-\frac{1}{2})+(\frac{1}{2}-\frac{1}{3})+…+(\frac{1}{n}-\frac{1}{n+1})]$=$2(1-\frac{1}{n+1})=\frac{2n}{n+1}$.
点评 本题考查求数列的通项,考查求数列的和,涉及到对数的运算性质等知识,分离分母且并项相加是解决本题的关键,注意解题方法的积累,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.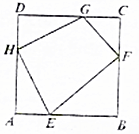 设四边形EFGH的四条边长为a,b,c,d,其四个顶点分别在单位正方形ABCD的四条边上,则2a2+b2+2c2+d2的最小值为( )
设四边形EFGH的四条边长为a,b,c,d,其四个顶点分别在单位正方形ABCD的四条边上,则2a2+b2+2c2+d2的最小值为( )
 设四边形EFGH的四条边长为a,b,c,d,其四个顶点分别在单位正方形ABCD的四条边上,则2a2+b2+2c2+d2的最小值为( )
设四边形EFGH的四条边长为a,b,c,d,其四个顶点分别在单位正方形ABCD的四条边上,则2a2+b2+2c2+d2的最小值为( )| A. | 3 | B. | 6 | C. | $3\sqrt{2}$ | D. | $\frac{8}{3}$ |
12.设实数x、y满足约束条件$\left\{\begin{array}{l}{3x-2y+4≥0}\\{x+y-4≤0}\\{x+ay-4≤0}\end{array}\right.$,已知z=2x+y的最大值是8,最小值是-5,则实数a的值为( )
| A. | 6 | B. | -6 | C. | -$\frac{1}{6}$ | D. | $\frac{1}{6}$ |
9.过双曲线 $\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1 (a>0,b>0)的一个焦点F向其一条渐近线作垂线l,垂足为A,l与另一条渐近线交于B点,若$\overrightarrow{FB}=2\overrightarrow{FA}$,则双曲线的离心率为( )
| A. | 2 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
 被圆
被圆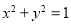 截得的弦长为
截得的弦长为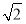 ,则
,则 ___________.
___________. 如图,在平面直角坐标系xOy中,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{{\sqrt{6}}}{3}$,直线l与x轴交于点E,与椭圆C交于A、B两点.当直线l垂直于x轴且点E为椭圆C的右焦点时,弦AB的长为$\frac{{2\sqrt{6}}}{3}$.
如图,在平面直角坐标系xOy中,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{{\sqrt{6}}}{3}$,直线l与x轴交于点E,与椭圆C交于A、B两点.当直线l垂直于x轴且点E为椭圆C的右焦点时,弦AB的长为$\frac{{2\sqrt{6}}}{3}$. 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,左、右焦点分别为F1,F2,点G在椭圆C上,且$\overrightarrow{G{F}_{1}}$•$\overrightarrow{G{F}_{2}}$=0,△GF1F2的面积为2.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,左、右焦点分别为F1,F2,点G在椭圆C上,且$\overrightarrow{G{F}_{1}}$•$\overrightarrow{G{F}_{2}}$=0,△GF1F2的面积为2.