题目内容
9.已知x1,x2(x1≠x2)是函数f(x)=ax3+bx2-a2x(a>0)的两个极值点.(Ⅰ)若x1=-1,x2=2,求函数f(x)的解析式;
(Ⅱ)若|x1|+|x2|=2$\sqrt{2}$,求实数b的最大值.
分析 (Ⅰ)求出原函数的导函数,由原函数有两个极值点,利用极值点处的导数等于0求得a,b的值,则函数解析式可求;
(Ⅱ)根据x1,x2(x1≠x2)是函数f(x)=ax3+bx2-a2x(a>0)的两个极值点,得到导函数的判别式大于0恒成立,再借助于根与系数关系得到x1,x2异号,由
|x1|+|x2|=2$\sqrt{2}$,得到a,b关系,把b看作关于a的函数后求导得到实数b的最大值.
解答 解:(Ⅰ)f′(x)=3ax2+2bx-a2(a>0).
∵x1=-1,x2=2是函数f(x)的两个极值点,
∴f′(-1)=0,f′(2)=0,
即3a-2b-a2=0,12a+4b-a2=0,解得a=6,b=-9.
∴f(x)=6x3-9x2-36x;
(Ⅱ)∵x1,x2(x1≠x2)是函数f(x)=ax3+bx2-a2x(a>0)的两个极值点,
∴${f}^{′}({x}_{1})={f}^{′}({x}_{2})=0$,
∴x1,x2是方程3ax2+2bx-a2=0(a>0)的两根,
则△=4b2+12a3>0对一切a>0,b∈R恒成立,
而${x}_{1}+{x}_{2}=-\frac{2b}{3a}$,x1x2=-$\frac{a}{3}$,又a>0,∴x1x2<0,
∴|x1|+|x2|=|x1-x2|=$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{(-\frac{2b}{3a})^{2}-4(-\frac{a}{3})}=\sqrt{\frac{4{b}^{2}}{9{a}^{2}}+\frac{4}{3}a}$,
由$|{x}_{1}|+|{x}_{2}|=2\sqrt{2}$,得$\sqrt{\frac{4{b}^{2}}{9{a}^{2}}+\frac{4}{3}a}=2\sqrt{2}$,
∴b2=3a2(6-a).
∵b2≥0,∴3a2(6-a)≥0,即0<a≤6.
令h(a)=3a2(6-a),则h′(a)=-9a2+36a.
当0<a<4时,h′(a)>0,∴h(a)在(0,4)上是增函数;
当4<a<6时,h′(a)<0,∴h(a)在(4,6)上是减函数.
∴当a=4时,h(a)有极大值为96,
即h(a)在(0,6]上的最大值是96,
∴b的最大值是4$\sqrt{6}$.
点评 本题考查利用导数研究函数的单调性,考查了利用导数求函数的最值,考查数学转化、化归等思想方法,训练了二次函数有两不等根条件的应用,是压轴题.

 阅读快车系列答案
阅读快车系列答案| A. | (1,2] | B. | [1,2] | C. | (-∞,-3)∪(1,+∞) | D. | [1,2) |
| A. | $\frac{{\sqrt{5}}}{5}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | 1 |
 如图,在平面直角坐标系xOy中,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{{\sqrt{6}}}{3}$,直线l与x轴交于点E,与椭圆C交于A、B两点.当直线l垂直于x轴且点E为椭圆C的右焦点时,弦AB的长为$\frac{{2\sqrt{6}}}{3}$.
如图,在平面直角坐标系xOy中,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{{\sqrt{6}}}{3}$,直线l与x轴交于点E,与椭圆C交于A、B两点.当直线l垂直于x轴且点E为椭圆C的右焦点时,弦AB的长为$\frac{{2\sqrt{6}}}{3}$.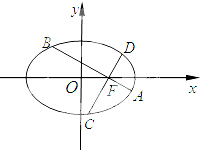 如图,在平面直角坐标系xoy中,椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,过椭圆右焦点F作两条互相垂直的弦AB与CD.当直线AB斜率为0时,|AB|+|CD|=5.
如图,在平面直角坐标系xoy中,椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,过椭圆右焦点F作两条互相垂直的弦AB与CD.当直线AB斜率为0时,|AB|+|CD|=5.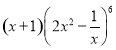 的展开式的常数项为_________________.
的展开式的常数项为_________________.