题目内容
10.在长方体ABCD-A1B1C1D1中,AB=$\sqrt{2}$,BC=AA1=1,点M为AB1的中点,点P为对角线AC1上的动点,点Q为底面ABCD上的动点(点P、Q可以重合),则MP+PQ的最小值为( )| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |
分析 画出图形,利用折叠与展开法则同一个平面,转化折线段为直线段距离最小,转化求解MP+PQ的最小值.
解答 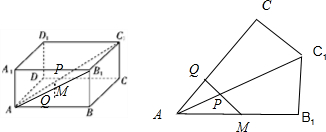 解:由题意,要求MP+PQ的最小值,就是P到底面ABCD的距离的最小值与MP的最小值之和,Q是P在底面上的射影距离最小,展开三角形ACC1与三角形AB1C1,在同一个平面上,如图,易知∠B1AC1=∠C1AC=30°,AM=$\frac{\sqrt{3}}{2}$,可知MQ⊥AC时,MP+PQ的最小,最小值为:$\frac{\sqrt{3}}{2}sin60°$=$\frac{3}{4}$.
解:由题意,要求MP+PQ的最小值,就是P到底面ABCD的距离的最小值与MP的最小值之和,Q是P在底面上的射影距离最小,展开三角形ACC1与三角形AB1C1,在同一个平面上,如图,易知∠B1AC1=∠C1AC=30°,AM=$\frac{\sqrt{3}}{2}$,可知MQ⊥AC时,MP+PQ的最小,最小值为:$\frac{\sqrt{3}}{2}sin60°$=$\frac{3}{4}$.
故选:C.
点评 本题考查最小值的求解,考查空间想象能力以及学生的计算能力,难度比较大.

练习册系列答案
相关题目
1.集合P={x|$\frac{x-1}{x+3}$>0},Q={x|y=$\sqrt{4-{x}^{2}}$},则P∩Q=( )
| A. | (1,2] | B. | [1,2] | C. | (-∞,-3)∪(1,+∞) | D. | [1,2) |
18.已知函数f(x)=x2-ax,g(x)=b+aln(x-1),存在实数a(a≥1),使y=f(x)的图象与y=g(x)的图象无公共点,则实数b的取值范围为( )
| A. | [1,+∞) | B. | [1,$\frac{3}{4}+ln2$) | C. | [$\frac{3}{4}+ln2,+∞$) | D. | (-$∞,\frac{3}{4}+ln2$) |
5.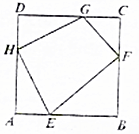 设四边形EFGH的四条边长为a,b,c,d,其四个顶点分别在单位正方形ABCD的四条边上,则2a2+b2+2c2+d2的最小值为( )
设四边形EFGH的四条边长为a,b,c,d,其四个顶点分别在单位正方形ABCD的四条边上,则2a2+b2+2c2+d2的最小值为( )
 设四边形EFGH的四条边长为a,b,c,d,其四个顶点分别在单位正方形ABCD的四条边上,则2a2+b2+2c2+d2的最小值为( )
设四边形EFGH的四条边长为a,b,c,d,其四个顶点分别在单位正方形ABCD的四条边上,则2a2+b2+2c2+d2的最小值为( )| A. | 3 | B. | 6 | C. | $3\sqrt{2}$ | D. | $\frac{8}{3}$ |
15.已知函数f(x)=3x(x∈R)的反函数为g(x),则g($\frac{1}{2}$)=( )
| A. | -log32 | B. | log32 | C. | -log23 | D. | log23 |
18.已知向量$\overrightarrow{a}$⊥$\overrightarrow{b}$,|$\overrightarrow{a}$-$\overrightarrow{b}$|=2,定义:cλ=λ$\overrightarrow{a}$+(1-λ)$\overrightarrow{b}$,其中0≤λ≤1.若${c_λ}•{c_{\frac{1}{2}}}=\frac{1}{2}$,则|cλ|的值不可能为( )
| A. | $\frac{{\sqrt{5}}}{5}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | 1 |
 :
: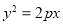 (
( )与椭圆
)与椭圆 :
: 相交所得的弦长为
相交所得的弦长为 .
. 的标准方程;
的标准方程; ,
, 是
是 上异于原点
上异于原点 的两个不同点,直线
的两个不同点,直线 和
和 的倾斜角分别为
的倾斜角分别为 和
和 ,当
,当 ,
, 变化且
变化且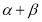 为定值
为定值 (
( )时,证明:直线
)时,证明:直线 恒过定点,并求出该定点的坐标.
恒过定点,并求出该定点的坐标.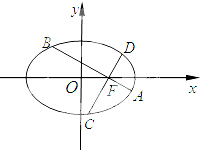 如图,在平面直角坐标系xoy中,椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,过椭圆右焦点F作两条互相垂直的弦AB与CD.当直线AB斜率为0时,|AB|+|CD|=5.
如图,在平面直角坐标系xoy中,椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,过椭圆右焦点F作两条互相垂直的弦AB与CD.当直线AB斜率为0时,|AB|+|CD|=5.