题目内容
13.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,短轴长为2.(Ⅰ)求椭圆C的方程;
(Ⅱ)若A、B是椭圆C上的两动点,O为坐标原点,OA、OB的斜率分别为k1,k2,问是否存在非零常数λ,使k1•k2=λ时,△AOB的面积S为定值,若存在,求λ的值;若不存在,请说明理由.
分析 (Ⅰ)通过$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$、2b=2、a2=b2+c2,计算即得结论;
(Ⅱ)设直线AB的方程并与椭圆方程联立,利用韦达定理、三角形面积计算公式、k1•k2=λ可得S△AOB的表达式,分析表达式、计算即可.
解答 解:(Ⅰ)∵e=$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$,2b=2,a2=b2+c2,
∴a=2,b=1,
∴椭圆C的方程为:$\frac{{x}^{2}}{4}$+y2=1;
(Ⅱ)结论:存在非零常数λ=-$\frac{1}{4}$,使k1•k2=-$\frac{1}{4}$时,△AOB的面积S为定值1.
理由如下:
设存在这样的常数λ,使k1•k2=λ时,S△AOB为定值.
设直线AB的方程为:y=kx+m,且AB与$\frac{{x}^{2}}{4}$+y2=1的交点坐标为A(x1,y1),B(x2,y2),
∵k1•k2=λ,∴λx1x2-y1y2=0,
∴-λx1x2+(kx1+m)(kx2+m)=0,
∴(k2-λ)x1x2+km(x1+x2)+m2=0.
将y=kx+m代入$\frac{{x}^{2}}{4}$+y2=1,消去y得:
(1+4k2)x2+8kmx+4m2-4=0,
由韦达定理可得:
x1+x2=$\frac{-8km}{1+4{k}^{2}}$,x1x2=$\frac{4{m}^{2}-4}{1+4{k}^{2}}$,
∴(k2-λ)x1x2+km(x1+x2)+m2=0可化为:m2=$\frac{4({k}^{2}-λ)}{1-4λ}$,
∵点O到直线AB的距离为d=$\frac{|m|}{\sqrt{1+{k}^{2}}}$,
∴S△AOB=$\frac{1}{2}$•d•|AB|=$\frac{1}{2}$•$\frac{|m|}{\sqrt{1+{k}^{2}}}$•$\sqrt{1+{k}^{2}}$•|x1-x2|=$\frac{1}{2}$•|x1-x2|•|m|=$\frac{2\sqrt{(1+4{k}^{2}){m}^{2}-{m}^{4}}}{1+4{k}^{2}}$,
∴$(\frac{{S}_{△AOB}}{2})^{2}$=$\frac{(1+4{k}^{2}){m}^{2}-{m}^{4}}{(1+4{k}^{2})^{2}}$
=$\frac{(1+4{k}^{2})•\frac{4({k}^{2}-λ)}{1-4λ}-\frac{16({k}^{2}-λ)^{2}}{(1-4λ)^{2}}}{(1+4{k}^{2})^{2}}$
=$\frac{(1+4{k}^{2})(4{k}^{2}-4λ)(1-4λ)-16({k}^{2}-λ)^{2}}{(1-4λ)^{2}(1+4{k}^{2})^{2}}$
=$\frac{-64λ{k}^{4}+(64{λ}^{2}+4){k}^{2}-4λ}{16{k}^{4}+8{k}^{2}+1}$•$\frac{1}{(1-4λ)^{2}}$,
要使△AOB的面积S为定值,只需$\frac{-64λ}{16}$=$\frac{64{λ}^{2}+4}{8}$=$\frac{-4λ}{1}$,
即只需(1+4λ)2=0,∴λ=-$\frac{1}{4}$,
此时$(\frac{{S}_{△AOB}}{2})^{2}$=$\frac{1}{4}$,即S△AOB=1,
故存在非零常数λ=-$\frac{1}{4}$,此时S△AOB=1.
点评 本题考查椭圆的定义及其标准方程、直线与椭圆的位置关系等基础知识,考查运算求解能力、抽象概括能力、推理论证能力,注意解题方法的积累,属于中档题.

| A. | (1,2] | B. | [1,2] | C. | (-∞,-3)∪(1,+∞) | D. | [1,2) |
| A. | [1,+∞) | B. | [1,$\frac{3}{4}+ln2$) | C. | [$\frac{3}{4}+ln2,+∞$) | D. | (-$∞,\frac{3}{4}+ln2$) |
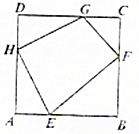 设四边形EFGH的四条边长为a,b,c,d,其四个顶点分别在单位正方形ABCD的四条边上,则2a2+b2+2c2+d2的最小值为( )
设四边形EFGH的四条边长为a,b,c,d,其四个顶点分别在单位正方形ABCD的四条边上,则2a2+b2+2c2+d2的最小值为( )| A. | 3 | B. | 6 | C. | $3\sqrt{2}$ | D. | $\frac{8}{3}$ |
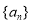 满足
满足
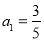 ,则数列的第2015项为_________.
,则数列的第2015项为_________.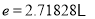 为自然对数的底数.
为自然对数的底数.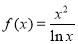 在区间
在区间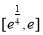 上的最值;
上的最值;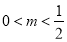 时,设函数
时,设函数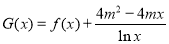 (其中
(其中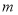 为常数)的3个极值点为
为常数)的3个极值点为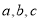 ,且
,且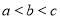 ,将
,将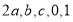 这5个数按照从小到大的顺序排列,并证明你的结论.
这5个数按照从小到大的顺序排列,并证明你的结论.