题目内容
9. 4月10日,2015《中国汉字听写大会》全国巡回赛正式启动,并拉开第三届“汉听大会”全国海选的帷幕.某市为了了解本市高中学生的汉字书写水平,在全市范围内随机抽取了近千名学生参加汉字听写考试,将所得数据整理后,绘制出频率分布直方图如图所示.
4月10日,2015《中国汉字听写大会》全国巡回赛正式启动,并拉开第三届“汉听大会”全国海选的帷幕.某市为了了解本市高中学生的汉字书写水平,在全市范围内随机抽取了近千名学生参加汉字听写考试,将所得数据整理后,绘制出频率分布直方图如图所示.(Ⅰ)求频率分布直方图中a的值,试估计全市学生参加汉字听写考试的平均成绩;
(Ⅱ)如果从参加本次考试的同学中随机选取1名同学,求这名同学考试成绩在80分以上的概率;
(Ⅲ)如果从参加本次考试的同学中随机选取3名同学,这3名同学中考试成绩在80分以上(含80分)的人数记为X,求X的分布列及数学期望.(注:频率可以视为相应的概率)
分析 (Ⅰ)利用概率和为1,可求a;根据频率分布直方图,计算数据的平均数即可;
(Ⅱ)计算被抽到的同学考试成绩在80(分)以上的概率;
(Ⅲ)得出X可能的取值,求出X的分布列与期望E(X).
解答 解:(Ⅰ)由题意,(2a+3a+7a+6a+2a)×10=1,∴a=0.005;
估计全市学生参加汉字听写考试的平均成绩为:
0.1×55+0.2×65+0.3×75+0.25×85+0.1×95=76.5…4分
(Ⅱ)(Ⅱ)设被抽到的这名同学考试成绩在80(分)以上为事件A.
P(A)=0.025×10+0.015×10=0.4;
∴被抽到的这名同学考试成绩在80(分)以上的概率为0.4; …(6分)
(Ⅲ)由(Ⅱ)知,从参加考试的同学中随机抽取1名同学的成绩在80(分)以上的概率为P=0.4;
X可能的取值是0,1,2,3;
∴P(X=0)=${C}_{3}^{0}•0.{4}^{0}•0.{6}^{3}$=$\frac{27}{125}$;
P(X=1)=${C}_{3}^{1}•0.4•0.{6}^{2}$=$\frac{54}{125}$;
P(X=2)=${C}_{3}^{2}•0.{4}^{2}•0.6$=$\frac{36}{125}$;
P(X=3)=${C}_{3}^{3}•0.{4}^{3}$=$\frac{8}{125}$.
∴X的分布列为:
| X | 0 | 1 | 2 | 3 |
| P | $\frac{27}{125}$ | $\frac{54}{125}$ | $\frac{36}{125}$ | $\frac{8}{125}$ |
所以 E(X)=0×$\frac{27}{125}$+1×$\frac{54}{125}$+2×$\frac{36}{125}$+3×$\frac{8}{125}$=$\frac{6}{5}$…(13分)
点评 本题考查了频率布直方图应用问题,也考查了离散型随机变量的分布列问题,是综合性题目.

练习册系列答案
相关题目
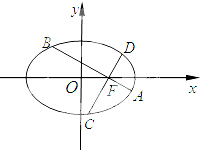 如图,在平面直角坐标系xoy中,椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,过椭圆右焦点F作两条互相垂直的弦AB与CD.当直线AB斜率为0时,|AB|+|CD|=5.
如图,在平面直角坐标系xoy中,椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,过椭圆右焦点F作两条互相垂直的弦AB与CD.当直线AB斜率为0时,|AB|+|CD|=5. 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,左、右焦点分别为F1,F2,点G在椭圆C上,且$\overrightarrow{G{F}_{1}}$•$\overrightarrow{G{F}_{2}}$=0,△GF1F2的面积为2.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,左、右焦点分别为F1,F2,点G在椭圆C上,且$\overrightarrow{G{F}_{1}}$•$\overrightarrow{G{F}_{2}}$=0,△GF1F2的面积为2.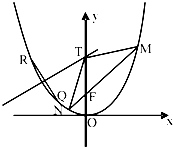 如图,过抛物线C:x2=2py(p>0)的焦点F的直线交C于M(x1,y1),N(x2,y2)两点,且x1x2=-4.
如图,过抛物线C:x2=2py(p>0)的焦点F的直线交C于M(x1,y1),N(x2,y2)两点,且x1x2=-4.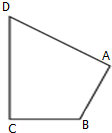 如图所示,在四边形ABCD中,|$\overrightarrow{CD}$|=4,|$\overrightarrow{AD}$|=5,$\overrightarrow{AB}$•$\overrightarrow{AD}$=$\overrightarrow{CB}$•$\overrightarrow{CD}$=0,令|$\overrightarrow{BC}$|=x,|$\overrightarrow{BA}$|=y,则曲线y=f(x)可能是( )
如图所示,在四边形ABCD中,|$\overrightarrow{CD}$|=4,|$\overrightarrow{AD}$|=5,$\overrightarrow{AB}$•$\overrightarrow{AD}$=$\overrightarrow{CB}$•$\overrightarrow{CD}$=0,令|$\overrightarrow{BC}$|=x,|$\overrightarrow{BA}$|=y,则曲线y=f(x)可能是( )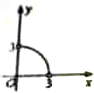

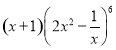 的展开式的常数项为_________________.
的展开式的常数项为_________________.