题目内容
【题目】已知函数f(x)=log2(x+2)与g(x)=(x﹣a)2+1,若对任意的x1∈[2,6),都存在x2∈[0,2],使得f(x1)=g(x2),则实数a的取值范围是 .
【答案】[﹣1,2﹣ ![]() ]∪[
]∪[ ![]() ,3]
,3]
【解析】解:∵x1∈[2,6),∴f(2)≤f(x1)<f(6),即2≤f(x1)<3,∴f(x1)的值域为[2,3).
g(x)的图象开口向上,对称轴为x=a,
1)若a≤0,则g(x)在[0,2]上是增函数,∴g(0)≤g(x2)≤g(2),即g(x2)的值域为[a2+1,a2﹣4a+5],
∴  ,解得﹣1≤a≤0.
,解得﹣1≤a≤0.
2)若a≥2,则g(x)在[0,2]上是减函数,∴g(2)≤g(x2)≤g(1),即g(x2)的值域为[a2﹣4a+5,a2+1],
∴ 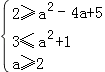 ,解得2≤a≤3.
,解得2≤a≤3.
3)若0<a≤1,则gmin(x)=g(a)=1,gmax(x)=g(2)=a2﹣4a+5,∴g(x)的值域为[1,a2﹣4a+5],
∴ ![]() ,解得0
,解得0 ![]() .
.
4)若1<a<2,则gmin(x)=g(a)=1,gmax(x)=g(0)=a2+1,∴g(x)的值域为[1,a2+1],
∴ ![]() ,解得
,解得 ![]() a<2.
a<2.
综上,a的取值范围是[﹣1,0]∪[2,3]∪(0,2﹣ ![]() )∪(
)∪( ![]() ,2)=[﹣1,2﹣
,2)=[﹣1,2﹣ ![]() ]∪[
]∪[ ![]() ,3].
,3].
所以答案是[﹣1,2﹣ ![]() ]∪[
]∪[ ![]() ,3].
,3].

练习册系列答案
相关题目





