题目内容
【题目】设函数
.
（1）当
时，
在
上恒成立，求实数
的取值范围；
（2）当
时，若函数
在
上恰有两个不同的零点，求实数
的取值范围；
【答案】（1）
；（2）
.
【解析】试题分析：（I）由
，我们可以由
在（1，+∞）上恒成立，得到
在
上恒成立，构造函数
，求出函数的最小值，即可得到实数m的取值范围；
（Ⅱ）当
时，我们易求出函数
，由方程的根与对应函数零点的关系，易转化为
在
上恰有两个不同的零点，利用导数分析函数的单调性，然后根据零点存在定理，构造关于
的不等式组，解不等式组即可得到答案．
试题解析：
（1）；（2）(
]
试题解析：（1）当时，由
得
，
∵
，∴
，∴有在上恒成立，
令
，由
得
，
当
，∴
在
上为减函数，在
上为增函数，
∴
，∴实数
的取值范围为；
（2）当时，函数，
在上恰有两个不同的零点，即在上恰有两个不同的零点，
令
，则
，
当
，
；当
，
，
∴
在
上单减，在
上单增，
，
又
，
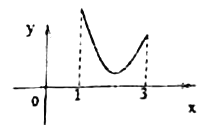
如图所示，
所以实数的取值范围为(]
练习册系列答案
阅读快车系列答案
相关题目
