题目内容
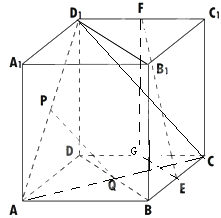
【题目】如图，在棱长为a的正方体ABCD﹣A1B1C1D1中，E，F，P，Q分别是BC，C1D1 ， AD1 ， BD的中点． 
（1）求证：PQ∥平面DCC1D1；
（2）求PQ的长；
（3）求证：EF∥平面BB1D1D．
【答案】
（1）证明：如图所示，连接AC，CD1，
∵P，Q分别为AD1、AC的中点，
∴PQ∥CD1，
∵CD1平面DCC1D1，PQ平面DCC1D1，
∴PQ∥平面DCC1D1
（2）解：由题意，可得：PQ= 
= 
（3）证明：取CD中点G，连结EG、FG，
∵E，F分别是BC，C1D1的中点，
∴FG∥D1D，EG∥BD，
又FG∩EG=G，
∴平面FGE∥平面BB1D1D，
∵EF平面FGE，
∴EF∥平面BB1D1D
【解析】（1）连接AC，CD1 ， 由P，Q分别为AD1、AC的中点，知PQ∥CD1 ， 由此能够证明PQ∥平面DCC1D1 ． （2）利用（1）的结论，直接求解即可．（3）取CD中点G，连结EG、FG，由已知得平面FGE∥平面BB1D1D，由此能证明EF∥平面BB1D1D．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
