Question

【题目】设函数f（x）=x2+ax+b，a，b∈R．
（1）若a+b=3，当x∈[1，2]时，f（x）≥0恒成立，求实数a的取值范围；
（2）是否存在实数对（a，b），使得不等式|f（x）|＞2在区间[1，5]上无解，若存在，试求出所有满足条件的实数对（a，b）；若不存在，请说明理由．

Answer 1

【答案】
（1）解：由f（x）≥0，即a（x﹣1）≥﹣（x2+3）．

当x=1时，恒成立；

当x∈（1，2]时，得 ，

令t=x﹣1∈（0，1]，

≤﹣7

综上：有a≥﹣7

（2）解：要使|f（x）|＞2在区间[1，5]上无解，

必须满足 ，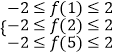

即

由 ，

相加得：﹣4≤8+2a≤4﹣6≤a≤2

再由 ，

相加得：﹣4≤16+2a≤4﹣10≤a≤﹣6

可以解得：a=﹣6，代入不等式组，得到b=7．

检验a=﹣6，时，|f（x）|≤2在区间[1，5]上恒成立

所以满足题意的是实数对（a，b）只有一对：（﹣6，7）

【解析】（1）分离参数得到 ，结合基本不等式的性质得到a的范围即可；（2）根据二次函数的性质得到关于a的不等式组，解出即可．