题目内容
【题目】甲,乙二人进行乒乓球比赛,已知每一局比赛甲胜乙的概率是![]() ,假设每局比赛结果相互独立.
,假设每局比赛结果相互独立.
(Ⅰ)比赛采用三局两胜制,即先获得两局胜利的一方为获胜方,这时比赛结束.求在一场比赛中甲获得比赛胜利的概率;
(Ⅱ)比赛采用三局两胜制,设随机变量![]() 为甲在一场比赛中获胜的局数,求
为甲在一场比赛中获胜的局数,求![]() 的分布列和均值;
的分布列和均值;
(Ⅲ)有以下两种比赛方案:方案一,比赛采用五局三胜制;方案二,比赛采用七局四胜制.问哪个方案对甲更有利.(只要求直接写出结果)
【答案】(Ⅰ)![]() (Ⅱ)分布列见解析,E(X)
(Ⅱ)分布列见解析,E(X)![]() (Ⅲ)方案二对甲更有利
(Ⅲ)方案二对甲更有利
【解析】
(Ⅰ)甲获得比赛胜利包含二种情况:①甲连胜二局;②前二局甲一胜一负,第三局甲胜.由此能求出甲获得比赛胜利的概率.
(Ⅱ)由已知得X的可能取值为0,1,2,分别求出相应的概率,由此能求出随机变量X的分布列和数学期望.
(Ⅲ)方案二对甲更有利.
(Ⅰ)甲获得比赛胜利包含二种情况:①甲连胜二局;②前二局甲一胜一负,第三局甲胜.
∴甲获得比赛胜利的概率为:
P=(![]() )2
)2![]() (
(![]() )
)![]() .
.
(Ⅱ)由已知得X的可能取值为0,1,2,
P(X=0)=(![]() )2
)2![]() ,
,
P(X=1)![]() ,
,
P(X=2)=(![]() )2
)2![]() (
(![]() )
)![]() .
.
∴随机变量X的分布列为:
X | 0 | 1 | 2 |
P |
|
|
|
∴数学期望E(X)![]() .
.
(Ⅲ)方案一,比赛采用五局三胜制;方案二,比赛采用七局四胜制.
方案二对甲更有利.

 名校课堂系列答案
名校课堂系列答案【题目】耐盐碱水稻俗称“海水稻”,是一种可以长在滩涂和盐碱地的水稻。还水稻的灌溉是将海水稀释后进行灌溉。某实验基础为了研究海水浓度![]() (
(![]() )对亩产量
)对亩产量![]() (吨)的影响,通过在试验田的种植实验,测得了某种还水稻的亩产量与海水浓度的数据如下表:
(吨)的影响,通过在试验田的种植实验,测得了某种还水稻的亩产量与海水浓度的数据如下表:
海水浓度 |
|
|
|
|
|
亩产量 |
|
|
|
|
|
绘制散点图发现,可用线性回归模型拟合亩产量![]() 与海水浓度
与海水浓度![]() 之间的相关关系,用最小二乘法计算得
之间的相关关系,用最小二乘法计算得![]() 与
与![]() 之间的线性回归方程为
之间的线性回归方程为![]() .
.
(1)求出![]() 的值,并估算当浇灌海水浓度为8%时该品种的亩产量。
的值,并估算当浇灌海水浓度为8%时该品种的亩产量。
(2)①完成下列残差表:
海水浓度 |
|
|
|
|
|
亩产量 |
|
|
|
|
|
| |||||
残差 |
②统计学中常用相关指数![]() 来刻画回归效果,
来刻画回归效果,![]() 越大,模型拟合效果越好,如假设
越大,模型拟合效果越好,如假设![]() ,就说明预报变量
,就说明预报变量![]() 的差异有
的差异有![]() 是由解释变量
是由解释变量![]() 引起的.请计算相关指数
引起的.请计算相关指数![]() (精确到0.01),并指出亩产量的变化多大程度上是由浇灌海水浓度引起的.
(精确到0.01),并指出亩产量的变化多大程度上是由浇灌海水浓度引起的.
(附:残差公式![]() ,相关指数
,相关指数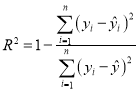 ,参考数据
,参考数据![]() )
)