题目内容
【题目】已知动圆
经过定点
，且与直线
相切，设动圆圆心的轨迹为曲线
.
（1）求曲线的方程；
（2）设过点
的直线
，
分别与曲线交于
，
两点，直线，的斜率存在，且倾斜角互补，证明：直线
的斜率为定值.
【答案】（1）
；（2）
【解析】
（1）由抛物线的定义可知E的轨迹为以D为焦点，以x=﹣1为准线的抛物线，
（2）设l1，l2的方程，联立方程组消元解出A，B的坐标，代入斜率公式计算kAB．
（1）由已知，动点
到定点
的距离等于到直线
的距离，由抛物线的定义知点的轨迹是以为焦点，以为准线的抛物线，故曲线
的方程为.
（2）由题意可知直线
，
的斜率存在，倾斜角互补，则斜率互为相反数，且不等于零.
设
，
，直线的方程为
，
.
直线的方程为
，
由
得
，
已知此方程一个根为
，∴
，
即
，同理
，
∴
，
，
∴
，
∴
，
所以，直线
的斜率为定值
.
练习册系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
第三学期赢在暑假系列答案
相关题目
【题目】为增强市民节能环保意识，某市面向全市征召义务宣传志愿者，现从符合条件的500名志愿者中随机抽取100名志愿者，他们的年龄情况如下表所示：
分组（单位：岁） | 频数 | 频率 |
| 5 | 0.05 |
| ① | 0.20 |
| 35 | ② |
| 30 | 0.30 |
| 10 | 0.10 |
总计 | 100 | 1.00 |
（1）频率分布表中的①②位置应填什么数据？
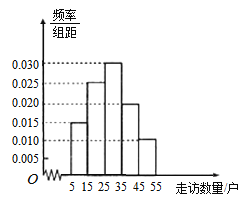
（2）补全如图所示的频率分布直方图，再根据频率分布直方图估计这500名志愿者中年龄在
岁的人数.
