Question

【题目】已知关于的方程， ，分别求满足下列条件实数的取值范围：

（1）有解；

（2）有唯一解；

（3）有两个解.

Answer 1

【答案】（1）；（2）；（3）

【解析】

（1）设，由指数函数的单调性，可得的范围，将方程化为在有解，设，求出在的值域，即可得到所求的范围．

（2）利用（1）的结果，通过函数的单调性与函数图象，求解方程只有一个解时的范围；

（3）利用函数的图象，写出由两个解时的范围．

（1）设，由，，可得，

方程，即为，

即在有解，

由，

当时，取得最小值，

，可得的最大值为60．

可得的最小值为，

的最大值为，

即有的取值范围是．

（2）由（1）可知在有解，

由，

时，是减函数，函数是增函数；

，是增函数，函数是减函数．

时，，时，，函数在的图象如图：

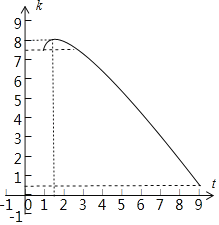
有唯一解；实数的取值范围：；

（3）有两个解，由图象可得实数的取值范围；