题目内容
13.已知△ABC是单位圆O的内接三角形,AD是圆的直径,若满足$\overrightarrow{AB}•\overrightarrow{AD}+\overrightarrow{AC}•\overrightarrow{AD}={\overrightarrow{BC}^2}$,则$|\overrightarrow{BC}|$=2.分析 如图所示,利用两个向量的加减法的法则,以及其几何意义、两个向量的数量积的定义化简$\overrightarrow{AB}•\overrightarrow{AD}$+$\overrightarrow{AC}•\overrightarrow{AD}$ 为4cos2β+4cos2α,△ABC中,由余弦定理可得 BC2=4cosβ2+4cos2α-2•2cosβ•2cosα•cos(α+β).再由由 $\overrightarrow{AB}•\overrightarrow{AD}+\overrightarrow{AC}•\overrightarrow{AD}={\overrightarrow{BC}^2}$,可得α+β=$\frac{π}{2}$,cosα=sinβ,从而求得$|\overrightarrow{BC}|$的值.
解答 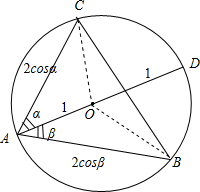 解:如图:设∠CAD=α,∠BAD=β,则|$\overrightarrow{AC}$|=2cosα,|$\overrightarrow{AB}$|=2cosβ.
解:如图:设∠CAD=α,∠BAD=β,则|$\overrightarrow{AC}$|=2cosα,|$\overrightarrow{AB}$|=2cosβ.
∵$\overrightarrow{AB}•\overrightarrow{AD}$+$\overrightarrow{AC}•\overrightarrow{AD}$=2$\overrightarrow{AO}$•$\overrightarrow{AB}$+2$\overrightarrow{AO}$•$\overrightarrow{AC}$=2•2cosβ•cosβ+2•2cosα•cosα=4cos2β+4cos2α,
△ABC中,由余弦定理可得 BC2=AB2+AC2-2AB•AC•cos(α+β)
=4cosβ2+4cos2α-2•2cosβ•2cosα•cos(α+β).
故由 $\overrightarrow{AB}•\overrightarrow{AD}+\overrightarrow{AC}•\overrightarrow{AD}={\overrightarrow{BC}^2}$,可得 4cos2β+4cos2α=4cosβ2+4cos2α-2•2cosβ•2cosα•cos(α+β),
∴cos(α+β)=0,α+β=$\frac{π}{2}$,∴cosα=sinβ,
∴则${\overrightarrow{BC}}^{2}$=4cos2β+4cos2α=4,∴$|\overrightarrow{BC}|$=2,
故答案为:2.
点评 本题主要考查两个向量的加减法的法则,以及其几何意义,两个向量的数量积的定义,余弦定理的应用,体现了数形结合的数学思想,属于中档题.

 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案| A. | x=$\frac{1}{16}$ | B. | y=$\frac{1}{16}$ | C. | y=$\frac{1}{32}$ | D. | x=$\frac{1}{32}$ |
| A. | x2+y2+10y=0 | B. | x2+y2-10y=0 | C. | x2+y2+10x=0 | D. | x2+y2-10x=0 |
| A. | 32 | B. | 64 | C. | 108 | D. | 128 |