题目内容
湖北省第十四届运动会纪念章委托某专营店销售,每枚进价5元,同时每销售一枚这种纪念章需向荆州筹委会交特许经营管理费2元,预计这种纪念章以每枚20元的价格销售时该店一年可销售2000枚,经过市场调研发现每枚纪念章的销售价格在每枚20元的基础上每减少一元则增加销售400枚,而每增加一元则减少销售100枚,现设每枚纪念章的销售价格为 元,
元, 为整数.
为整数.
(1)写出该专营店一年内销售这种纪念章所获利润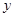 (元)与每枚纪念章的销售价格
(元)与每枚纪念章的销售价格 (元)的函数关系式(并写出这个函数的定义域);
(元)的函数关系式(并写出这个函数的定义域);
(2)当每纪念章销售价格 为多少元时,该特许专营店一年内利润
为多少元时,该特许专营店一年内利润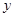 (元)最大,并求出最大值.
(元)最大,并求出最大值.
(1)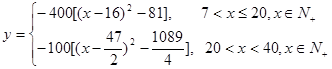 ,定义域为
,定义域为
(2)当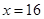 时,该特许专营店获得的利润最大为32400元.
时,该特许专营店获得的利润最大为32400元.
解析试题分析:此题主要考查学生对函数模型在实际问题中应用的能力.(1)在此类问题中要注意单价与销售量之间的相关关系,同时要注意单价价格的取值范围,必要时要进行分段列式,再根据题意求解;(2)经审题实际问题是求函数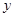 的最大值,由(1)可知函数
的最大值,由(1)可知函数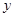 是分段函数,所以要在自变量的各区间中求出最大值,进行比较,从而求出函数的最大值,再还原回实际问题的解.
是分段函数,所以要在自变量的各区间中求出最大值,进行比较,从而求出函数的最大值,再还原回实际问题的解.
试题解析:(1)依题意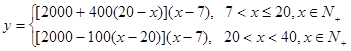
∴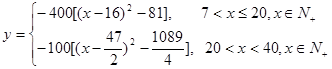 ,
,
定义域为 6分
6分
(2)∵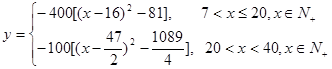 ,]
,]
∴当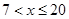 时,则
时,则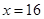 ,
,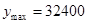 (元)
(元)
当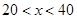 时,则
时,则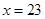 或24,
或24, (元)
(元)
综上:当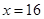 时,该特许专营店获得的利润最大为32400元. 12分
时,该特许专营店获得的利润最大为32400元. 12分
考点:1.实际问题中的函数建模;2.分段函数的最值;3.二次函数的最值.

练习册系列答案
相关题目
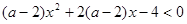 对一切
对一切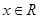 恒成立,试确定实数
恒成立,试确定实数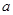 的取值范围.
的取值范围. 是定义在
是定义在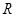 上的奇函数,当
上的奇函数,当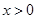 时的解析式为
时的解析式为 .
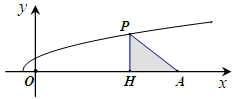
.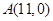 ,函数
,函数 的图象上的动点
的图象上的动点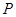 在
在 轴上的射影为
轴上的射影为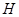 ,且点
,且点 的左侧.设
的左侧.设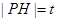 ,
,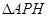 的面积为
的面积为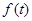 .
.
 的取值范围;
的取值范围;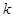 米的圆.在这个圆上安装座位,且每个座位和圆心处的支点都有一根直的钢管相连.经预算,摩天轮上的每个座位与支点相连的钢管的费用为
米的圆.在这个圆上安装座位,且每个座位和圆心处的支点都有一根直的钢管相连.经预算,摩天轮上的每个座位与支点相连的钢管的费用为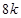 元/根,且当两相邻的座位之间的圆弧长为
元/根,且当两相邻的座位之间的圆弧长为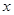 米时,相邻两座位之间的钢管和其中一个座位的总费用为
米时,相邻两座位之间的钢管和其中一个座位的总费用为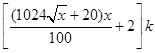 元.假设座位等距离分布,且至少有两个座位,所有座位都视为点,且不考虑其他因素,记摩天轮的总造价为
元.假设座位等距离分布,且至少有两个座位,所有座位都视为点,且不考虑其他因素,记摩天轮的总造价为 元.
元.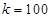 米时,试确定座位的个数,使得总造价最低?
米时,试确定座位的个数,使得总造价最低?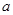 为实数,函数
为实数,函数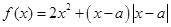 .
.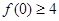 ,求
,求 的最小值.
的最小值. 毫克)与时间
毫克)与时间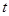 (小时)成正比;药物释放完毕后,
(小时)成正比;药物释放完毕后,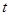 的函数关系式为
的函数关系式为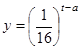 (
(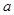 为常数),如图所示,根据图中提供的信息,回答下列问题:
为常数),如图所示,根据图中提供的信息,回答下列问题: