题目内容
某公园准备建一个摩天轮,摩天轮的外围是一个周长为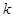 米的圆.在这个圆上安装座位,且每个座位和圆心处的支点都有一根直的钢管相连.经预算,摩天轮上的每个座位与支点相连的钢管的费用为
米的圆.在这个圆上安装座位,且每个座位和圆心处的支点都有一根直的钢管相连.经预算,摩天轮上的每个座位与支点相连的钢管的费用为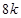 元/根,且当两相邻的座位之间的圆弧长为
元/根,且当两相邻的座位之间的圆弧长为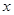 米时,相邻两座位之间的钢管和其中一个座位的总费用为
米时,相邻两座位之间的钢管和其中一个座位的总费用为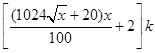 元.假设座位等距离分布,且至少有两个座位,所有座位都视为点,且不考虑其他因素,记摩天轮的总造价为
元.假设座位等距离分布,且至少有两个座位,所有座位都视为点,且不考虑其他因素,记摩天轮的总造价为 元.
元.
(Ⅰ)试写出 关于
关于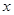 的函数关系式,并写出定义域;
的函数关系式,并写出定义域;
(Ⅱ)当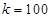 米时,试确定座位的个数,使得总造价最低?
米时,试确定座位的个数,使得总造价最低?
(Ⅰ)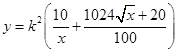 ,
,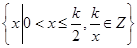 (Ⅱ)当座位个数为
(Ⅱ)当座位个数为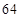 个
个
解析试题分析:(Ⅰ)根据题意,相邻的两座位之间的弧长为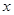 米,则可推出摩天轮的总座位数
米,则可推出摩天轮的总座位数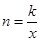 ,摩天轮的造价分成座位与支点相连的钢管的费用和两座位之间的钢管和其中一个座位的费用两部分之和,即:
,摩天轮的造价分成座位与支点相连的钢管的费用和两座位之间的钢管和其中一个座位的费用两部分之和,即: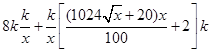 ,化简整理得到
,化简整理得到 关于
关于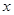 的函数关系式,又由题中所给至少有两个座位可得
的函数关系式,又由题中所给至少有两个座位可得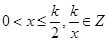 ;(Ⅱ)由
;(Ⅱ)由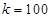 米时,可对(Ⅰ)中的函数进一步化简成
米时,可对(Ⅰ)中的函数进一步化简成 关于
关于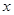 的函数关系式
的函数关系式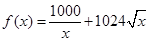 ,根据其特点可对函数进行求导,之后令
,根据其特点可对函数进行求导,之后令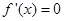 ,求得对应的
,求得对应的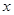 值,从而求出函数
值,从而求出函数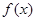 最小值.
最小值.
试题解析:解:(Ⅰ)设摩天轮上总共有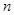 个座位,则
个座位,则 ,即
,即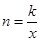 ,
,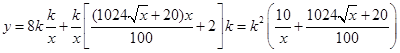 ,(3分)
,(3分)
定义域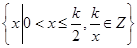 ; (6分)
; (6分)
(Ⅱ)当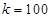 时,令
时,令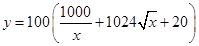
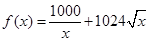 ,
,
则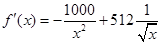
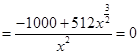 ,
,
∴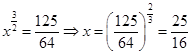 ,(11分)
,(11分)
当 时,
时,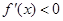 ,即
,即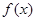 在
在 上单调减,
上单调减,
当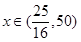 时,
时,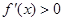 ,即
,即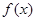 在
在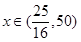 上单调增,
上单调增,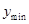 在
在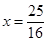 时取到,此时座位个数为
时取到,此时座位个数为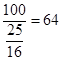 个. (16分)
个. (16分)
考点:1.函数应用题;2.导数求函数的最值

练习册系列答案
相关题目
 元.公司拟投入
元.公司拟投入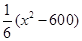 万元作为技改费用,投入50万元作为固定宣传费用,投入
万元作为技改费用,投入50万元作为固定宣传费用,投入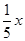 万元作为浮动宣传费用.试问:当该商品明年的销售量
万元作为浮动宣传费用.试问:当该商品明年的销售量 至少应达到多少万件时,才可能使明年的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.
至少应达到多少万件时,才可能使明年的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.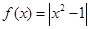 ,
,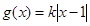 .
.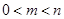 ,若
,若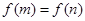 ,求
,求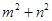 的值;
的值; ,当
,当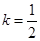 时,求
时,求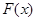 在
在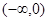 上的最小值;
上的最小值; 在区间
在区间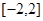 上的最大值.
上的最大值.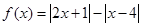 .
.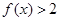 ;
;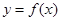 的最小值.
的最小值. 元,
元,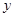 (元)与每枚纪念章的销售价格
(元)与每枚纪念章的销售价格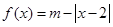 ,
,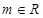 ,且
,且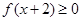 的解集为
的解集为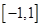 .
.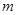 的值;
的值;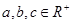 ,且
,且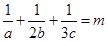 ,求证:
,求证: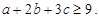
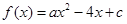 ,且
,且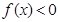 的解集是(1,5).
的解集是(1,5). 在
在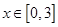 上的值域.
上的值域.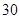 天内每件的销售价格
天内每件的销售价格 (元)与时间
(元)与时间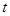 (天)的函数关系是
(天)的函数关系是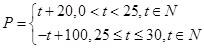 该商品的日销售量
该商品的日销售量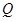 (件)与时间
(件)与时间
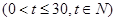 ,设商品的日销售额为
,设商品的日销售额为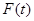 (销售量与价格之积)
(销售量与价格之积) 为实数,记函数
为实数,记函数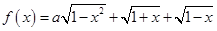 的最大值为
的最大值为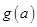 .
.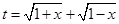 ,求
,求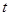 的取值范围,并把
的取值范围,并把 表示为
表示为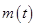 ;
;