题目内容
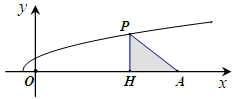
如图,已知点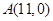 ,函数
,函数 的图象上的动点
的图象上的动点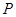 在
在 轴上的射影为
轴上的射影为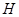 ,且点
,且点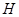 在点
在点 的左侧.设
的左侧.设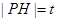 ,
,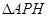 的面积为
的面积为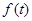 .
.
(Ⅰ)求函数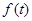 的解析式及
的解析式及 的取值范围;
的取值范围;
(Ⅱ)求函数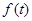 的最大值.
的最大值.
(Ⅰ)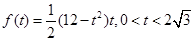 ;(Ⅱ)8.
;(Ⅱ)8.
解析试题分析:(Ⅰ)根据已知条件,需要表示出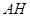 和
和 ,因为
,因为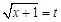 ,所以点
,所以点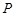 的横坐标为
的横坐标为 ,
,
而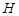 在点
在点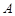 的左侧,所以
的左侧,所以 ,即
,即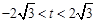 ,由已知
,由已知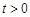 ,所以
,所以 ,则
,则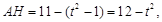 所以
所以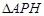 的面积为
的面积为 ;(Ⅱ)
;(Ⅱ)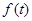 是关于t的三次函数,要求它的最大值,用导数的方法求解,
是关于t的三次函数,要求它的最大值,用导数的方法求解,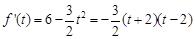 ,由
,由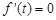 ,得
,得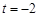 (舍),或
(舍),或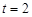 . 根据函数单调性情况,知当
. 根据函数单调性情况,知当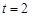 时,函数
时,函数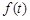 取得最大值8.
取得最大值8.
试题解析:(Ⅰ)由已知可得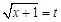 ,所以点
,所以点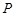 的横坐标为
的横坐标为 ,
,
因为点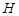 在点
在点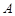 的左侧,所以
的左侧,所以 ,即
,即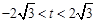 .
.
由已知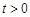 ,所以
,所以 ,
,
所以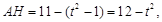
所以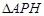 的面积为
的面积为 .
.
(Ⅱ)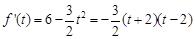
由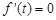 ,得
,得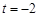 (舍),或
(舍),或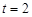 .
.
函数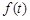 与
与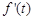 在定义域上的情况如下:
在定义域上的情况如下:
所以当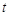
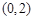
2 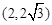
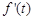
+ 0 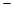
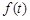
↗ 极大值 ↘ 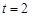 时,函数
时,函数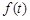 取得最大值8.
取得最大值8.
考

练习册系列答案
相关题目
某市电力公司在电力供不应求时期,为了居民节约用电,采用“阶梯电价”方法计算电价,每月用电不超过 度时,按每度
度时,按每度 元计费,每月用电超过
元计费,每月用电超过 度时,超过部分按每度
度时,超过部分按每度 元计费,每月用电超过
元计费,每月用电超过 度时,超过部分按每度
度时,超过部分按每度 元计费
元计费
(Ⅰ)设每月用电 度,应交电费
度,应交电费 元,写出
元,写出 关于
关于 的函数;
的函数;
(Ⅱ)已知小王家第一季度缴费情况如下:
| 月份 | 1 | 2 | 3 | 合计 |
| 缴费金额 | 87元 | 62元 | 45元8角 | 194元8角 |
 .
.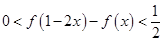 ,当
,当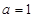 时,求
时,求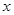 的取值范围;
的取值范围;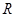 上奇函数
上奇函数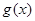 满足
满足 ,且当
,且当 时,
时,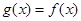 ,求
,求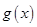 在
在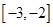 上的反函数
上的反函数 ;
;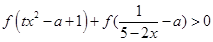 在区间
在区间 上有解,求实数
上有解,求实数 的取值范围.
的取值范围. ; (2)
; (2)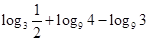 .
.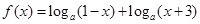
 的定义域和值域;
的定义域和值域;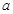 的值.
的值. 元,
元,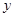 (元)与每枚纪念章的销售价格
(元)与每枚纪念章的销售价格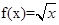 (0<x≤1),求x∈[-5,-4]时,函数f(x)的解析式.
(0<x≤1),求x∈[-5,-4]时,函数f(x)的解析式. 的值;
的值; 的值.
的值.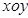 ,则股价
,则股价 (元)和时间
(元)和时间 的关系在
的关系在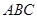 段可近似地用解析式
段可近似地用解析式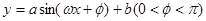 来描述,从
来描述,从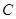 点走到今天的
点走到今天的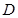 点,是震荡筑底阶段,而今天出现了明显的筑底结束的标志,且
点,是震荡筑底阶段,而今天出现了明显的筑底结束的标志,且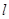 :
: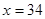 对称。老张预计这只股票未来的走势如图中虚线所示,这里
对称。老张预计这只股票未来的走势如图中虚线所示,这里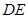 段与
段与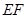 段是股价延续
段是股价延续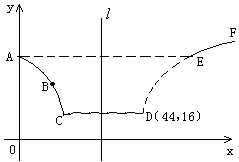
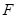 。现在老张决定取点
。现在老张决定取点
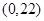 ,点
,点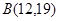 ,点
,点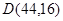 来确定解析式中的常数
来确定解析式中的常数 ,
,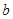 ,
,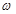 ,
,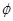 ,并且求得
,并且求得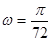 。
。