题目内容
对定义在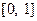 上,并且同时满足以下两个条件的函数
上,并且同时满足以下两个条件的函数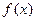 称为
称为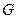 函数。
函数。
① 对任意的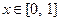 ,总有
,总有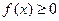 ;
;
② 当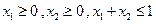 时,总有
时,总有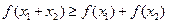 成立。
成立。
已知函数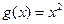 与
与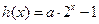 是定义在
是定义在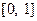 上的函数。
上的函数。
(1)试问函数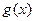 是否为
是否为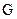 函数?并说明理由;
函数?并说明理由;
(2)若函数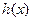 是
是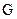 函数,求实数
函数,求实数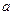 组成的集合;
组成的集合;
(3)在(2)的条件下,讨论方程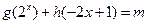
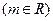 解的个数情况。
解的个数情况。
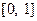 上,并且同时满足以下两个条件的函数
上,并且同时满足以下两个条件的函数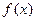 称为
称为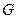 函数。
函数。① 对任意的
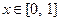 ,总有
,总有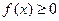 ;
;② 当
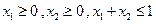 时,总有
时,总有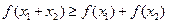 成立。
成立。已知函数
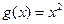 与
与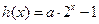 是定义在
是定义在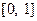 上的函数。
上的函数。(1)试问函数
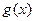 是否为
是否为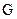 函数?并说明理由;
函数?并说明理由;(2)若函数
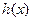 是
是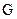 函数,求实数
函数,求实数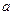 组成的集合;
组成的集合;(3)在(2)的条件下,讨论方程
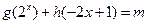
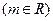 解的个数情况。
解的个数情况。(1) 当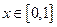 时,总有
时,总有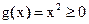 ,满足①,
,满足①,
当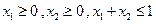 时,
时,
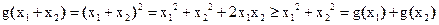 ,满足②
,满足②
(2)若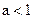 时,
时,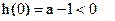 不满足①,所以不是
不满足①,所以不是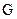 函数;
函数;
若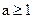 时,
时,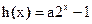 ,在
,在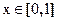 上是增函数,
上是增函数,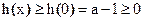 ,满足①
,满足①
由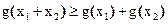 ,得
,得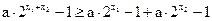 ,即
,即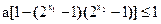 ,
,
因为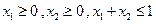 所以
所以 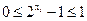
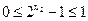
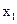 与
与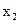 不同时等于1
不同时等于1
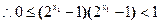
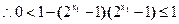

当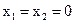 时,
时,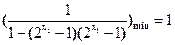
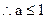 , 综合上述:
, 综合上述: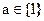
(3)根据(2)知: a=1,方程为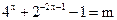 ,
,
令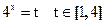 方程为
方程为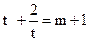 当
当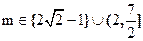 时,有一解;
时,有一解;
当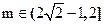 时,有二不同解;当
时,有二不同解;当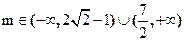 时,方程无
时,方程无
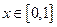 时,总有
时,总有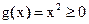 ,满足①,
,满足①,当
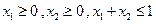 时,
时,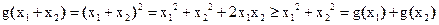 ,满足②
,满足②(2)若
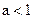 时,
时,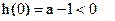 不满足①,所以不是
不满足①,所以不是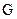 函数;
函数;若
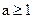 时,
时,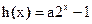 ,在
,在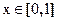 上是增函数,
上是增函数,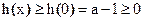 ,满足①
,满足①由
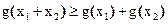 ,得
,得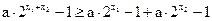 ,即
,即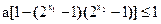 ,
,因为
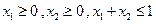 所以
所以 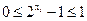
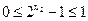
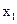 与
与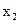 不同时等于1
不同时等于1 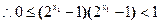
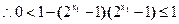

当
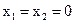 时,
时,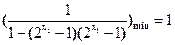
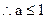 , 综合上述:
, 综合上述: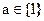
(3)根据(2)知: a=1,方程为
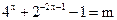 ,
,令
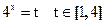 方程为
方程为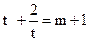 当
当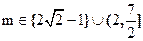 时,有一解;
时,有一解;当
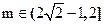 时,有二不同解;当
时,有二不同解;当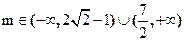 时,方程无
时,方程无同答案

练习册系列答案
 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案 小学学习好帮手系列答案
小学学习好帮手系列答案
相关题目
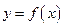 在
在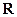 上是奇函数,而且在
上是奇函数,而且在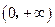 上是增函数,
上是增函数,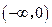 上也是增函数.
上也是增函数.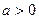 ,
,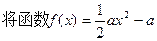 的图象向右平移
的图象向右平移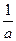 个单位再向下平移
个单位再向下平移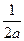 个单位后得到函数
个单位后得到函数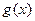 的图象。
的图象。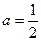 时,求
时,求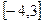 上的最大值与最小值;
上的最大值与最小值;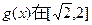 上的最小值为
上的最小值为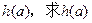 的最大值。
的最大值。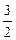 x2 ..
x2 ..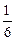 ,
,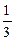 ],不等式|a-lnx|-ln[ f ’(x)+3x]>0成立,求实数a的取值范围;
],不等式|a-lnx|-ln[ f ’(x)+3x]>0成立,求实数a的取值范围; 在
在 上是减函数,求
上是减函数,求 的取值集合.
的取值集合. 、
、 时,定义
时,定义 =
= ,则函数
,则函数
 的单调递减区间是( ).
的单调递减区间是( ).

 和
和
 和
和
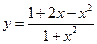 的值域.
的值域.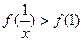 的实数x的取值范围是
的实数x的取值范围是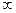 ,1)
,1)
 (0,1)
(0,1) 是偶函数,则
是偶函数,则 的递减区间是 .
的递减区间是 .