题目内容
19.证明:(1+x)2n展开式中xn的系数等于(1+x)2n-1展开式中xn的系数的2倍.分析 利用二项式定理展开,即可得出结论.
解答 证明:(1+x)2n=1+C2n1•x+C2n2x2+…+C2nnxn+…+C2n2nx2n,
其中xn的系数设为A,则A=C2nn=2n(2n-1)(2n-2)…(n+1)÷n!
(1+x)2n-1=1+C2n-11x+C2n-12x2+…+C2n-1nxn+…+C2n-12n-1x2n-1,
其中xn的系数设为B,则B=C2n-1n=(2n-1)(2n-2)(2n-3)…(n-1+1)÷n!
因为A>0,B>0,A÷B=2n÷n=2
所以A=2B,原命题得证
点评 本题考查二项式定理,考查学生分析解决问题的能力,比较基础.

练习册系列答案
相关题目
9.已知$\overrightarrow{a}$=(4,3),$\overrightarrow{b}$=(-2,1),如果$λ\overrightarrow{a}$-$\overrightarrow{b}$与$\overrightarrow{b}$垂直,则|$\overrightarrow{a}$-λ$\overrightarrow{b}$|的值为( )
| A. | 1 | B. | $\sqrt{5}$ | C. | 5 | D. | 2$\sqrt{5}$ |
10.已知变量x,y满足不等式组$\left\{\begin{array}{l}x+2y-1≥0\\ 2x+y-2≤0\\ x-y+2≥0\end{array}$.,则Z=8x•2y的最小值为( )
| A. | 2 | B. | 1 | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
7.已知全集U=R,集合A={x|y=log2(x2+3x-10)},B={x|-2≤x≤5},则(∁UA)∩B等于( )
| A. | {x|-5<x≤2} | B. | {x|-2<x≤5} | C. | {x|-2≤x≤2} | D. | {x|-5≤x≤5} |
9.已知两个不同的平面α,β和两条不重合的直线m,n,则下列命题正确的是( )
| A. | 若m∥n,n?α,则m∥α | B. | 若α⊥β,α∩β=n,m⊥n,则m⊥β | ||
| C. | 若m?α,n?α,m∥β,n∥β,则α∥β | D. | 若m⊥β,m?α,则α⊥β |
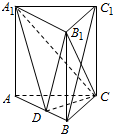 已知三棱柱ABC-A1B1C1中,侧棱垂直于底面,AC=BC,点D是AB的中点.求证:
已知三棱柱ABC-A1B1C1中,侧棱垂直于底面,AC=BC,点D是AB的中点.求证: