题目内容
9.已知两个不同的平面α,β和两条不重合的直线m,n,则下列命题正确的是( )| A. | 若m∥n,n?α,则m∥α | B. | 若α⊥β,α∩β=n,m⊥n,则m⊥β | ||
| C. | 若m?α,n?α,m∥β,n∥β,则α∥β | D. | 若m⊥β,m?α,则α⊥β |
分析 利用线面平行、线面垂直、面面平行、面面垂直的判定定理分别分析选择.
解答 解:对于A,若m∥n,n?α,则m∥α或m?α,所以A不正确.
对于B,若α⊥β,α∩β=n,m⊥n,则m⊥β,或m?β,或m?β,所以B不正确.
对于C,若m?α,n?α,m∥β,n∥β,则α∥β或α∩β=l,所以C不正确.
对于D,若m⊥β,m?α,则α⊥β,满足平面与平面垂直的判定定理,所以D正确.
故选:D.
点评 本题考查平面与平面的位置关系的判断,直线与平面的位置关系的判断,基本知识的考查.

练习册系列答案
相关题目
19.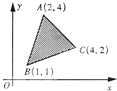 已知A(2,4),B(1,1),C(4,2).给出平面区域为三角形ABC的内部及其边界,若使目标函数z=ax+y(a>0)取得最大值的最优解有无穷多个,则a值等于( )
已知A(2,4),B(1,1),C(4,2).给出平面区域为三角形ABC的内部及其边界,若使目标函数z=ax+y(a>0)取得最大值的最优解有无穷多个,则a值等于( )
 已知A(2,4),B(1,1),C(4,2).给出平面区域为三角形ABC的内部及其边界,若使目标函数z=ax+y(a>0)取得最大值的最优解有无穷多个,则a值等于( )
已知A(2,4),B(1,1),C(4,2).给出平面区域为三角形ABC的内部及其边界,若使目标函数z=ax+y(a>0)取得最大值的最优解有无穷多个,则a值等于( )| A. | $\frac{1}{3}$ | B. | 6 | C. | 3 | D. | 1 |
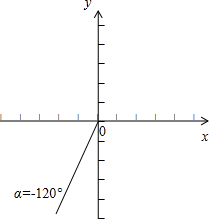 .
.