题目内容

14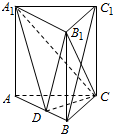．已知三棱柱ABC-A1B1C1中，侧棱垂直于底面，AC=BC，点D是AB的中点．求证：
（1）平面CA1D⊥平面AA1B1B；
（2）BC1∥平面CA1D．

分析 （1）根据面面垂直的判定定理即可证明平面CA1D⊥平面AA1B1B；
（2）根据线面平行的判定定理即可证明BC1∥平面CA1D．

解答 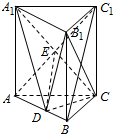证明：（1）由AC=BC，D是AB的中点，得AB⊥CD，
由AA1⊥面ABC，得AA1⊥CD，
∵AA1∩AB=A
∴CD⊥面AA1B1B，
∵CD?平面CA1D，
∴平面CA1D⊥平面AA1B1B．
（2）连接AC1交A1C于点E，连接DE
因为四边形AA1C1C是矩形，知E为AC1的中点
又D是AB的中点，得到DE∥BC1，
从而可得BC1∥面CA1D．

点评 本题主要考查空间直线和平面平行，平面和平面垂直的判定，根据相应的定理是解决本题的关键．

练习册系列答案
相关题目
4．计算：lg0.01+（$\frac{1}{8}$）${\;}^{\frac{1}{3}}$=-$\frac{3}{2}$．
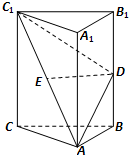5．如图，在直三棱柱ABC-A1B1C1中，AB=BC，D，E分别为BB1，AC1的中点．
（1）证明：DE⊥平面ACC1A1；
（2）设AA1=AC=$\sqrt{2}$AB，求二面角A1-AD-C1的大小．
2．计算复数$\frac{1-i}{3+i}$=$\frac{1}{5}-\frac{2}{5}i$．
9．${（1-\sqrt{x}）^5}$的展开式中x2的系数是（　　）
A．-5B．5C．-10D．10
19．证明：（1+x）2n展开式中xn的系数等于（1+x）2n-1展开式中xn的系数的2倍．
6．直线x-y-4=0上有一点P，它与两定点A（1，1）、B（2，3）的距离相等，则点P的坐标是（$\frac{9}{2}，\frac{1}{2}$）．
3．已知在△ABC中，a=2，∠A=$\frac{π}{3}$．
（1）求面积的最大值；
（2）求周长的最大值；
（3）若三角形为锐角三角形，求周长的取值范围；
（4）求b+2c的取值范围；
（5）$\frac{sinB}{cosC}$＞$\sqrt{3}$，求∠C的取值范围．
4．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0），两个焦点分别为F1，F2．
（1）若|F1F2|=2，点P在椭圆上，且△PF1F2的周长为6，求椭圆C的方程；
（2）动圆Γ：x2+y2=R2，其中b＜R＜a，若A是椭圆C上的动点，B是动圆Γ上的动点，且直线AB与椭圆C和动圆Γ均相切，求A、B两点的距离|AB|的最大值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网