题目内容
已知a>0,函数f(x)=-2asin(2x+ )+2a+b,当x∈[0,
)+2a+b,当x∈[0,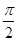 ]时,-5≤f(x)≤1.
]时,-5≤f(x)≤1.
(1)求常数a,b的值;
(2)设g(x)=f(x+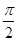 )且lg[g(x)]>0,求g(x)的单调区间.
)且lg[g(x)]>0,求g(x)的单调区间.
 )+2a+b,当x∈[0,
)+2a+b,当x∈[0,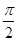 ]时,-5≤f(x)≤1.
]时,-5≤f(x)≤1.(1)求常数a,b的值;
(2)设g(x)=f(x+
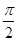 )且lg[g(x)]>0,求g(x)的单调区间.
)且lg[g(x)]>0,求g(x)的单调区间.(1)a=2,b=-5
(2)综上,g(x)的递增区间为(kπ,kπ+ ](k∈Z);递减区间为(kπ+
](k∈Z);递减区间为(kπ+ ,kπ+
,kπ+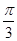 )(k∈Z).
)(k∈Z).
(2)综上,g(x)的递增区间为(kπ,kπ+
 ](k∈Z);递减区间为(kπ+
](k∈Z);递减区间为(kπ+ ,kπ+
,kπ+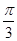 )(k∈Z).
)(k∈Z).解:(1)∵x∈[0,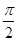 ],
],
∴2x+ ∈[
∈[ ,
,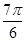 ].
].
∴sin(2x+ )∈[-
)∈[-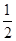 ,1],
,1],
又∵a>0,
∴-2asin(2x+ )∈[-2a,a].
)∈[-2a,a].
∴f(x)∈[b,3a+b],
又∵-5≤f(x)≤1,
∴b=-5,3a+b=1,
因此a=2,b=-5.
(2)由(1)得a=2,b=-5,
∴f(x)=-4sin(2x+ )-1,
)-1,
g(x)=f(x+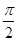 )=-4sin(2x+
)=-4sin(2x+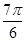 )-1=4sin(2x+
)-1=4sin(2x+ )-1,
)-1,
又由lg[g(x)]>0,得g(x)>1,
∴4sin(2x+ )-1>1,
)-1>1,
∴sin(2x+ )>
)>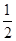 ,
,
∴2kπ+ <2x+
<2x+ <2kπ+
<2kπ+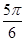 ,k∈Z,
,k∈Z,
其中当2kπ+ <2x+
<2x+ ≤2kπ+
≤2kπ+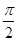 ,k∈Z时,g(x)单调递增,即kπ<x≤kπ+
,k∈Z时,g(x)单调递增,即kπ<x≤kπ+ ,k∈Z,
,k∈Z,
∴g(x)的单调增区间为(kπ,kπ+ ],k∈Z.
],k∈Z.
又∵当2kπ+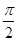 <2x+
<2x+ <2kπ+
<2kπ+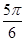 ,k∈Z时,g(x)单调递减,
,k∈Z时,g(x)单调递减,
即kπ+ <x<kπ+
<x<kπ+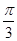 ,k∈Z.
,k∈Z.
∴g(x)的单调减区间为(kπ+ ,kπ+
,kπ+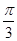 ),k∈Z.
),k∈Z.
综上,g(x)的递增区间为(kπ,kπ+ ](k∈Z);递减区间为(kπ+
](k∈Z);递减区间为(kπ+ ,kπ+
,kπ+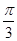 )(k∈Z).
)(k∈Z).
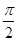 ],
],∴2x+
 ∈[
∈[ ,
,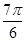 ].
].∴sin(2x+
 )∈[-
)∈[-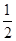 ,1],
,1],又∵a>0,
∴-2asin(2x+
 )∈[-2a,a].
)∈[-2a,a].∴f(x)∈[b,3a+b],
又∵-5≤f(x)≤1,
∴b=-5,3a+b=1,
因此a=2,b=-5.
(2)由(1)得a=2,b=-5,
∴f(x)=-4sin(2x+
 )-1,
)-1,g(x)=f(x+
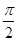 )=-4sin(2x+
)=-4sin(2x+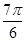 )-1=4sin(2x+
)-1=4sin(2x+ )-1,
)-1,又由lg[g(x)]>0,得g(x)>1,
∴4sin(2x+
 )-1>1,
)-1>1,∴sin(2x+
 )>
)>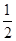 ,
,∴2kπ+
 <2x+
<2x+ <2kπ+
<2kπ+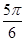 ,k∈Z,
,k∈Z,其中当2kπ+
 <2x+
<2x+ ≤2kπ+
≤2kπ+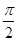 ,k∈Z时,g(x)单调递增,即kπ<x≤kπ+
,k∈Z时,g(x)单调递增,即kπ<x≤kπ+ ,k∈Z,
,k∈Z,∴g(x)的单调增区间为(kπ,kπ+
 ],k∈Z.
],k∈Z.又∵当2kπ+
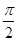 <2x+
<2x+ <2kπ+
<2kπ+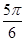 ,k∈Z时,g(x)单调递减,
,k∈Z时,g(x)单调递减,即kπ+
 <x<kπ+
<x<kπ+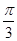 ,k∈Z.
,k∈Z.∴g(x)的单调减区间为(kπ+
 ,kπ+
,kπ+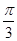 ),k∈Z.
),k∈Z.综上,g(x)的递增区间为(kπ,kπ+
 ](k∈Z);递减区间为(kπ+
](k∈Z);递减区间为(kπ+ ,kπ+
,kπ+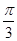 )(k∈Z).
)(k∈Z).
练习册系列答案
相关题目
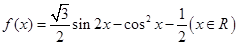
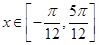 时,求函数
时,求函数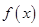 取得最大值和最小值时
取得最大值和最小值时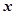 的值;
的值;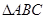 的内角A、B、C的对应边分别是
的内角A、B、C的对应边分别是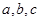 ,且
,且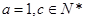 ,若向量
,若向量 与向量
与向量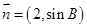 平行,求
平行,求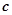 的值.
的值. 的最小值是( )
的最小值是( )




 )的图象向左平移φ个单位,得到偶函数g(x)的图象,则φ的最小正值为( )
)的图象向左平移φ个单位,得到偶函数g(x)的图象,则φ的最小正值为( )


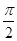 )与g(x)=cos(ωx-
)与g(x)=cos(ωx-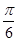 )(ω>0)的图象具有相同的对称中心,则φ=( )
)(ω>0)的图象具有相同的对称中心,则φ=( )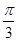
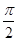 )上的函数y=6cosx的图象与y=5tanx的图象交于点P,过点P作x轴的垂线,垂足为P1,直线PP1与函数y=sinx的图象交于点P2,则线段P1P2的长为________.
)上的函数y=6cosx的图象与y=5tanx的图象交于点P,过点P作x轴的垂线,垂足为P1,直线PP1与函数y=sinx的图象交于点P2,则线段P1P2的长为________.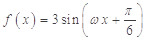 ,
,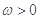 ,
,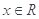 ,且以
,且以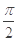 为最小正周期.
为最小正周期.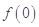 ;
;
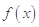 的解析式;
的解析式;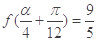 ,求
,求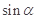 的值.
的值.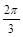 x+
x+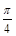 )的最小正周期是 .
)的最小正周期是 .